11. định lý Bayes

Spread the love

Định lý Bayes là công thức dùng để tính xác suất xảy ra của một biến cố dựa trên thông tin đã biết về một biến cố khác. Nó cho phép ta cập nhật niềm tin khi có dữ liệu mới.

📘 Công thức định lý Bayes

Cho hai biến cố A và B, với $P(B) > 0$ , định lý Bayes phát biểu:

$P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$

Trong đó:

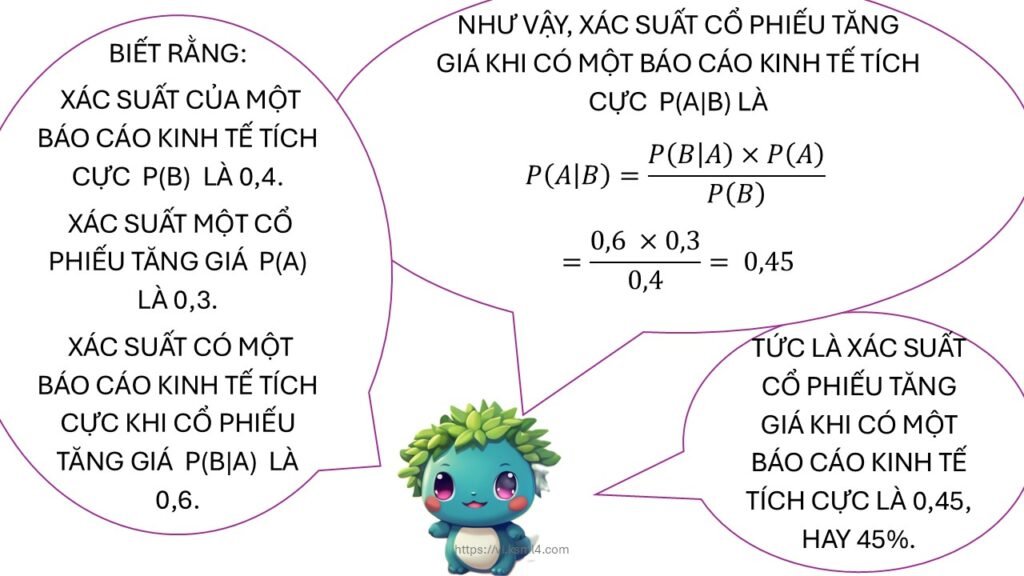
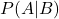$P(A|B)$ : xác suất xảy ra A khi biết B đã xảy ra (xác suất hậu nghiệm)
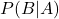$P(B|A)$ : xác suất xảy ra B khi A đã xảy ra (xác suất điều kiện)
$P(A)$ : xác suất ban đầu của A (xác suất tiên nghiệm)
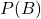$P(B)$ : xác suất xảy ra của B

🧠 Ý nghĩa thực tế

Định lý Bayes giúp ta cập nhật xác suất của một giả thuyết khi có thêm bằng chứng. Nó là nền tảng của thống kê Bayes, được ứng dụng rộng rãi trong:

Y học: chẩn đoán bệnh dựa trên kết quả xét nghiệm
Machine Learning: phân loại dữ liệu, học có giám sát
Kinh tế học: dự báo thị trường dựa trên dữ liệu mới
An ninh mạng: phát hiện gian lận hoặc tấn công
Ra quyết định: đánh giá rủi ro khi có thông tin bổ sung

🧪 Ví dụ thực tế: Chẩn đoán bệnh

Giả sử:

1% dân số mắc bệnh X → $P(A) = 0.01$
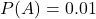
Xét nghiệm cho kết quả dương tính đúng 99% nếu mắc bệnh → $P(B|A) = 0.99$
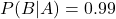
Xét nghiệm cho kết quả dương tính sai 5% nếu không mắc bệnh → $P(B|\bar{A}) = 0.05$

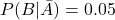
👉 Tính xác suất thực sự mắc bệnh khi có kết quả dương tính:

$P(A|B) = \frac{0.99 \cdot 0.01}{0.99 \cdot 0.01 + 0.05 \cdot 0.99} = \frac{0.0099}{0.0099 + 0.0495} \approx 0.166$

🔍 Kết luận: Dù xét nghiệm dương tính, xác suất thực sự mắc bệnh chỉ khoảng 16.6% → cần xét nghiệm bổ sung.

🧪 1. Y học: Chẩn đoán bệnh dựa trên kết quả xét nghiệm

Tình huống:
Một bệnh hiếm gặp có tỷ lệ mắc là 1% trong dân số. Xét nghiệm có:

Độ nhạy (dương tính khi mắc bệnh): 99%
Độ đặc hiệu (âm tính khi không mắc bệnh): 95%

Câu hỏi: Nếu một người có kết quả xét nghiệm dương tính, xác suất thực sự mắc bệnh là bao nhiêu?

Giả sử:

A: biến cố “người đó mắc bệnh”
B: biến cố “người đó có kết quả xét nghiệm dương tính”

Khi đó, công thức định lý Bayes:

$P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$

Giải thích:

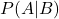$P(A|B)$ : xác suất người đó mắc bệnh khi biết rằng họ có kết quả dương tính
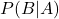$P(B|A)$ : xác suất có kết quả dương tính nếu người đó mắc bệnh (độ nhạy của xét nghiệm)
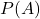$P(A)$ : xác suất ban đầu người đó mắc bệnh (tỷ lệ mắc bệnh trong dân số)
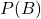$P(B)$ : xác suất có kết quả dương tính (tổng xác suất dương tính từ cả người bệnh và không bệnh)

👉 Kết quả: khoảng 16.6% — cho thấy rằng dù xét nghiệm dương tính, khả năng mắc bệnh vẫn thấp → cần xét nghiệm bổ sung.

📈 2. Kinh tế học: Dự báo thị trường dựa trên dữ liệu mới

Tình huống:
Một nhà đầu tư muốn biết khả năng thị trường tăng khi có tin tức tích cực về lãi suất.

P( thị trường tăng) = 0.4
P( tin tích cực| thị trường tăng) = 0.7
P( tin tích cực) = 0.5

Áp dụng định lý Bayes:
P( thị trường tăng| tin tích cực) $= \frac{0.7 \cdot 0.4}{0.5} = 0.56$

👉 Nhà đầu tư có thể cập nhật chiến lược dựa trên xác suất mới: 56% khả năng thị trường tăng khi có tin tích cực.

🔐 3. An ninh mạng: Phát hiện gian lận hoặc tấn công

Tình huống:
Một hệ thống giám sát phát hiện hành vi bất thường trong truy cập tài khoản.

Xác suất tài khoản bị tấn công: 0.01
Xác suất hệ thống cảnh báo khi có tấn công: 0.95
Xác suất hệ thống cảnh báo khi không có tấn công: 0.05

Câu hỏi: Nếu hệ thống cảnh báo, xác suất thực sự có tấn công là bao nhiêu?

👉 Áp dụng định lý Bayes → kết quả khoảng 16%
→ Giúp chuyên viên an ninh đánh giá mức độ nghiêm trọng và quyết định phản ứng phù hợp.

🧠 4. Ra quyết định: Đánh giá rủi ro khi có thông tin bổ sung

Tình huống:
Một công ty đang cân nhắc đầu tư vào một dự án. Ban đầu, xác suất thành công là 60%. Sau khi nhận được báo cáo phân tích tích cực, họ muốn cập nhật xác suất thành công.

P( báo cáo tích cực| thành công) = 0.9
P( báo cáo tích cực| thất bại) = 0.3
P( thành công) = 0.6

👉 Áp dụng định lý Bayes → xác suất thành công sau khi có báo cáo tích cực tăng lên khoảng 81.8%

→ Giúp ban lãnh đạo ra quyết định đầu tư với niềm tin được cập nhật.

Discover more from Cùng Học Cùng Mơ

Subscribe to get the latest posts sent to your email.