7. Xác suất của phần hợp

Spread the love

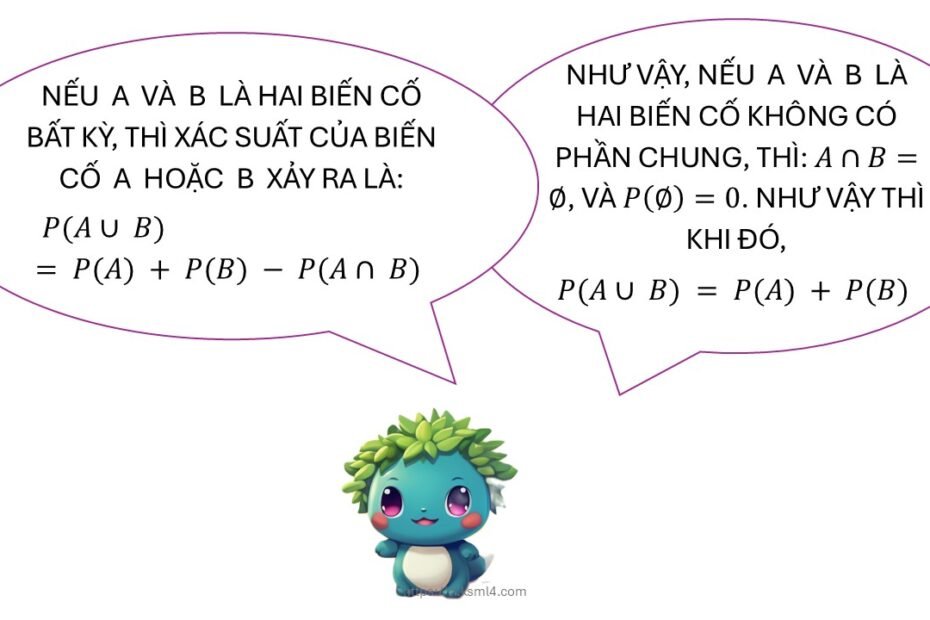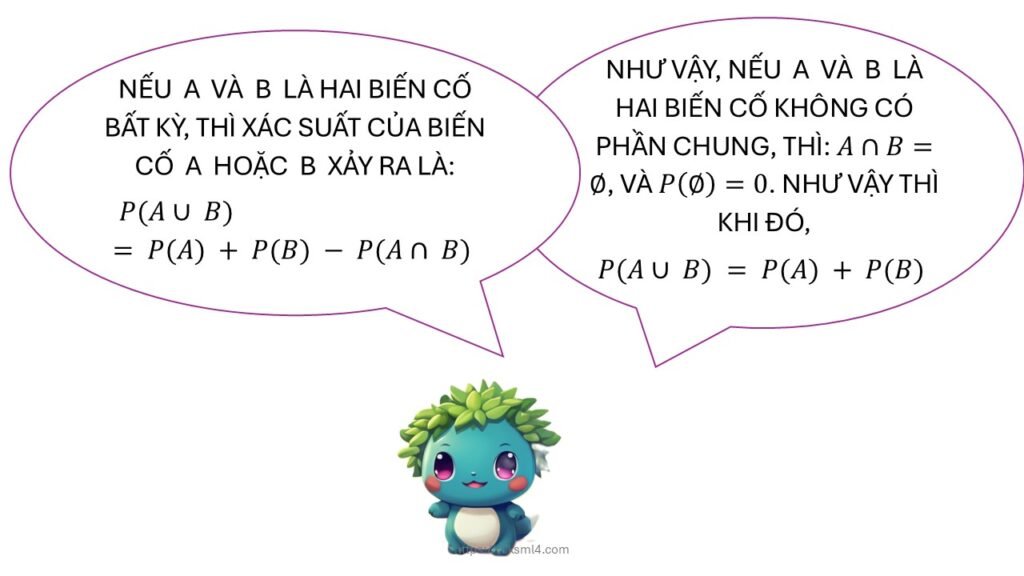
Xác suất của phần hợp hai biến cố A và B được tính bằng công thức:

$P(A \cup B) = P(A) + P(B) - P(A \cap B)$

Công thức này giúp tránh đếm trùng phần giao giữa A và B.

📘 Giải thích chi tiết

Trong xác suất, phần hợp $A \cup B$ là biến cố xảy ra khi ít nhất một trong hai biến cố A hoặc B xảy ra.

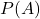$P(A)$ : xác suất xảy ra của biến cố A
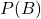$P(B)$ : xác suất xảy ra của biến cố B
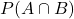$P(A \cap B)$ : xác suất xảy ra đồng thời của cả A và B

👉 Nếu A và B xung khắc (không thể xảy ra cùng lúc), thì $P(A \cap B) = 0$ , và công thức trở thành:

$P(A \cup B) = P(A) + P(B)$

📌 Ví dụ minh họa

🎲 Ví dụ 1: Tung xúc xắc

Tung một viên xúc xắc 6 mặt. Gọi:

A: ra số chẵn → {2, 4, 6} → $P(A) = \frac{3}{6} = 0.5$
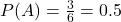
B: ra số lớn hơn 3 → {4, 5, 6} → $P(B) = \frac{3}{6} = 0.5$
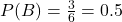
A ∩ B: số vừa chẵn vừa lớn hơn 3 → {4, 6} → $P(A \cap B) = \frac{2}{6}$

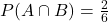
Áp dụng công thức:

$P(A \cup B) = 0.5 + 0.5 - \frac{2}{6} = 1 - \frac{1}{3} = \frac{2}{3}$

🧠 Ứng dụng thực tế

Phân tích rủi ro: Tính xác suất xảy ra ít nhất một sự cố trong hệ thống
Bài toán xác suất trong thi cử: Xác suất làm đúng ít nhất một câu hỏi
Xác suất trong bảo hiểm: Tính khả năng xảy ra ít nhất một loại tổn thất

🎓 1. Thi đậu ít nhất một môn

Bài toán: Một học sinh thi 2 môn: Toán và Văn.

Xác suất đậu Toán: $P(A) = 0.7$
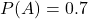
Xác suất đậu Văn: $P(B) = 0.6$
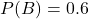
Xác suất đậu cả hai môn: $P(A \cap B) = 0.5$

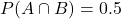
👉 Xác suất đậu ít nhất một môn là:

$P(A \cup B) = 0.7 + 0.6 - 0.5 = 0.8$

🟢 Có 80% khả năng học sinh đậu ít nhất một môn.

🎲 2. Trò chơi rút thăm trúng thưởng

Bài toán: Một công ty tổ chức rút thăm với 2 giải:

Giải A: xác suất trúng là 0.2
Giải B: xác suất trúng là 0.3
Có 0.1 xác suất trúng cả hai giải

👉 Xác suất trúng ít nhất một giải:

$P(A \cup B) = 0.2 + 0.3 - 0.1 = 0.4$

🛒 3. Khách hàng mua ít nhất một sản phẩm

Bài toán: Trong một ngày:

60% khách mua sản phẩm A
50% khách mua sản phẩm B
30% khách mua cả hai

👉 Xác suất khách mua ít nhất một sản phẩm:

$P(A \cup B) = 0.6 + 0.5 - 0.3 = 0.8$

✈️ 4. Hành khách đến đúng giờ

Bài toán:

Xác suất đến đúng giờ bằng xe buýt: 0.6
Xác suất đến đúng giờ bằng tàu điện: 0.5
Xác suất đến đúng giờ bằng cả hai: 0.3

👉 Xác suất đến đúng giờ bằng ít nhất một phương tiện:

$P(A \cup B) = 0.6 + 0.5 - 0.3 = 0.8$

Discover more from Cùng Học Cùng Mơ

Subscribe to get the latest posts sent to your email.