Bất đẳng thức liên quan đến giá trị tuyệt đối là một chủ đề thú vị trong toán học. Các bất đẳng thức này thường xuất phát từ các tính chất của giá trị tuyệt đối và được sử dụng để giải bài toán, phân tích khoảng cách, hoặc xử lý các biểu thức phức tạp. Dưới đây là các bất đẳng thức quan trọng và ví dụ minh họa:
Không âm
![]() cho mọi số thực
cho mọi số thực ![]() .
.
- Giá trị tuyệt đối luôn “tích cực” hoặc bằng 0, như một người bạn luôn lạc quan! 😎
Ví dụ: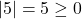 ,
, 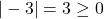 ,
, 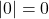 .
.
Giá trị tuyệt đối và số 0: ![]() .
.
- Chỉ khi
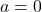 , giá trị tuyệt đối mới bằng 0. Nếu
, giá trị tuyệt đối mới bằng 0. Nếu 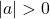 , thì
, thì 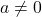 .
.
Ví dụ: Nếu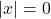 , thì
, thì 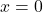 . Nếu
. Nếu 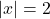 , thì
, thì 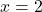 hoặc
hoặc 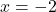 .
.
Nếu ![]() , với
, với ![]() , thì
, thì ![]() hoặc
hoặc ![]() .
.
Giá trị tuyệt đối ![]() nghĩa là
nghĩa là ![]() cách số 0 đúng
cách số 0 đúng ![]() đơn vị trên trục số. Vì vậy,
đơn vị trên trục số. Vì vậy, ![]() có thể ở hai vị trí:
có thể ở hai vị trí:
Bên phải: ![]() (khoảng cách
(khoảng cách ![]() từ 0 về phía dương).
từ 0 về phía dương).
Bên trái: ![]() (khoảng cách
(khoảng cách ![]() từ 0 về phía âm).
từ 0 về phía âm).
Cứ tưởng tượng như bạn đứng ở gốc 0, rồi đi ![]() bước sang phải (
bước sang phải (![]() ) hoặc sang trái (
) hoặc sang trái (![]() ), bạn vẫn cách gốc đúng
), bạn vẫn cách gốc đúng ![]() bước! 🚶♂️
bước! 🚶♂️
Ví dụ:
- Nếu
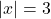 , thì
, thì 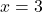 hoặc
hoặc 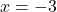 .
. - Kiểm tra:
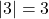 ,
, 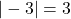 . Đúng!
. Đúng! - Nếu
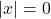 , thì
, thì 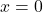 (vì chỉ có
(vì chỉ có 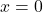 thỏa mãn
thỏa mãn 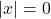 ).
). - Nếu
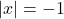 , thì không có nghiệm, vì giá trị tuyệt đối không bao giờ âm (không có
, thì không có nghiệm, vì giá trị tuyệt đối không bao giờ âm (không có 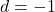 ).
).
Lưu ý:
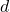 phải không âm (
phải không âm (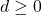 ), vì
), vì 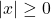 .
.- Nếu gặp phương trình dạng
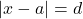 , thì
, thì 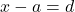 hoặc
hoặc 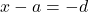 , dẫn đến
, dẫn đến 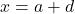 hoặc
hoặc 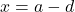 .
.
Bất đẳng thức tam giác
Công thức: ![]() cho mọi
cho mọi ![]() thực.
thực.
- Nghĩa là giá trị tuyệt đối của tổng hai số không vượt quá tổng giá trị tuyệt đối của chúng. Giống như đi đường tắt (
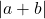 ) bao giờ cũng nhanh hơn hoặc bằng đi vòng (
) bao giờ cũng nhanh hơn hoặc bằng đi vòng (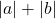 ). Ví dụ: Với
). Ví dụ: Với 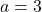 ,
, 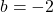 :
:
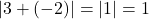 .
.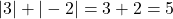 .
.- Kiểm tra:
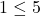 , đúng!
, đúng!
Mở rộng: Với nhiều số, ta có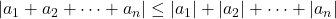 .
.
Dạng tổng quát hơn: ![]() .
.
- Đây là bất đẳng thức ngược, cho biết khoảng cách giữa
 và
và 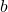 ít nhất bằng hiệu của giá trị tuyệt đối của chúng. Ví dụ: Với
ít nhất bằng hiệu của giá trị tuyệt đối của chúng. Ví dụ: Với 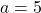 ,
, 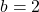 :
:
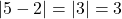 .
.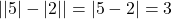 .
.- Kiểm tra:
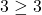 , đúng!
, đúng!
Bất đẳng thức liên quan đến khoảng cách
Công thức: ![]() là khoảng cách giữa
là khoảng cách giữa ![]() và
và ![]() trên trục số.
trên trục số.
- Bất đẳng thức này thường được dùng để diễn tả khoảng cách hoặc điều kiện về khoảng cách. Ví dụ: Nếu
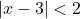 , nghĩa là
, nghĩa là 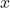 cách
cách 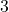 không quá 2 đơn vị.
không quá 2 đơn vị.
- Giải:
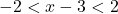 .
. - Cộng 3:
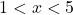 .
. - Nghĩa là
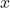 nằm trong khoảng
nằm trong khoảng 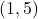 , như bạn đứng gần tiệm trà sữa trong bán kính 2 bước! 🧋
, như bạn đứng gần tiệm trà sữa trong bán kính 2 bước! 🧋
- Giải:
Bất đẳng thức với tích và thương
Tích: ![]() .
.
- Giá trị tuyệt đối của tích bằng tích các giá trị tuyệt đối.
Ví dụ: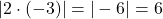 , và
, và 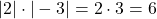 .
.
Thương: ![]() (với
(với ![]() ).
).
Ví dụ: ![]() , và
, và ![]() .
.
Bất đẳng thức: Nếu ![]() , thì
, thì ![]() (với
(với ![]() ).
).
Ví dụ: Nếu ![]() , thì với
, thì với ![]() , ta có
, ta có ![]() , tức
, tức ![]() .
.
Giải bất đẳng thức giá trị tuyệt đối
Bất đẳng thức giá trị tuyệt đối thường xuất hiện dưới dạng ![]() ,
, ![]() ,
, ![]() , hoặc
, hoặc ![]() . Cách giải dựa trên ý nghĩa khoảng cách.
. Cách giải dựa trên ý nghĩa khoảng cách.
Dạng ![]() :
:
- Nghĩa là
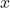 cách
cách  nhỏ hơn
nhỏ hơn 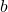 .
. - Giải:
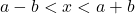 . Ví dụ:
. Ví dụ: 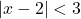 .
.
- Giải:
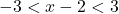 .
. - Cộng 2:
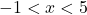 .
. - Nghĩa là
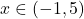 .
.
- Giải:
Dạng ![]() :
:
- Nghĩa là
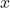 cách
cách  lớn hơn
lớn hơn 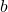 .
. - Giải:
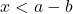 hoặc
hoặc 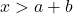 . Ví dụ:
. Ví dụ: 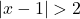 .
.
- Giải:
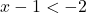 hoặc
hoặc 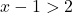 .
. - Cộng 1:
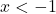 hoặc
hoặc 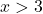 .
. - Nghĩa là
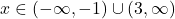 .
.
- Giải:
Bất đẳng thức dạng tổng quát
Dạng ![]() :
:
- Giải:
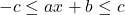 . Ví dụ:
. Ví dụ: 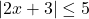 .
.
- Giải:
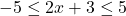 .
. - Trừ 3:
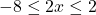 .
. - Chia 2:
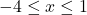 .
. - Nghĩa là
![Rendered by QuickLaTeX.com x \in [-4, 1]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-74561a639da82788989afc7a2e095ef7_l3.png) .
.
- Giải:
Dạng ![]() :
:
- Giải:
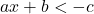 hoặc
hoặc 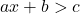 . Ví dụ:
. Ví dụ: 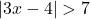 .
.
- Giải:
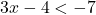 hoặc
hoặc 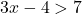 .
. - Cộng 4:
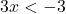 hoặc
hoặc 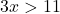 .
. - Chia 3:
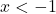 hoặc
hoặc 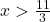 .
. - Nghĩa là
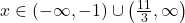 .
.
- Giải:
Ứng dụng vui:
- Bất đẳng thức giá trị tuyệt đối hay được dùng để mô tả “vùng an toàn” (như bạn đứng gần tiệm trà sữa trong bán kính 2km) hoặc “vùng nguy hiểm” (như tránh xa khu vực nào đó quá 5km). 🚶♂️
- Trong thực tế, nó còn xuất hiện trong lập trình, xử lý sai số, hoặc đo khoảng cách trong không gian.