Các quy tắc tính giới hạn

Spread the love

⚡ 1. Quy tắc thế trực tiếp

Nếu hàm số “ngoan ngoãn” tại điểm $x = a$ , tức là không chia cho 0 hoặc gặp dạng vô định, thì cứ thế vào thôi.

Ví dụ: $\lim_{x \to 2} (3x + 1) = 3 \cdot 2 + 1 = 7$

💬 Giải thích vui: Hàm hiền lành, không gây rối, thì cứ việc thế vô, như gọi tên người quen!

✅ Ví dụ 1:

Tính:

$\lim_{x \to 2} (x^2 + 3x - 1)$

📌 Giải: Thế trực tiếp luôn →

$= 2^2 + 3 \cdot 2 - 1 = 4 + 6 - 1 = 9$

🎉 Kết quả: 9

✅ Ví dụ 2:

Tính:

$\lim_{x \to -1} (\sqrt{x^2 + 2x + 2})$

📌 Giải: Thế trực tiếp luôn →

$= \sqrt{(-1)^2 + 2(-1) + 2} = \sqrt{1 - 2 + 2} = \sqrt{1} = 1$

🔍 2. Quy tắc khử dạng vô định

Khi thế vào mà ra 0/0 hoặc ∞/∞ thì đừng hoảng! Dùng các kỹ thuật sau để “giải cứu giới hạn”:

✂️ Rút gọn biểu thức

Ví dụ: $\lim_{x \to 2} \frac{x^2 - 4}{x - 2} = \lim_{x \to 2} \frac{(x - 2)(x + 2)}{x - 2} = \lim_{x \to 2} x + 2 = 4$

💬 Giải thích vui: Giống như dọn dẹp phòng – bỏ mấy thứ thừa ra mới thấy được kết quả!

🧩 Nhân liên hợp (khi có căn)

Ví dụ: $\lim_{x \to 0} \frac{\sqrt{x + 1} - 1}{x}$ → nhân liên hợp để phá “vô định”

💬 Giải thích vui: Nhân liên hợp là chiêu “cân bằng lực lượng” khi căn số chơi trò giấu mặt.

🔁 Ví dụ 1:

Tính:

$\lim_{x \to 3} \frac{x^2 - 9}{x - 3}$

📌 Nhận dạng:

Thay vào: $\frac{9 - 9}{0} = \frac{0}{0}$ → dạng vô định

📌 Phân tích:

$x^2 - 9 = (x - 3)(x + 3)$
→ $\frac{(x - 3)(x + 3)}{x - 3} = x + 3$
⇒ $\lim_{x \to 3} x + 3 = 6$

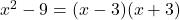
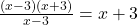
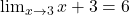
🔁 Ví dụ 2:

Tính:

$\lim_{x \to 1} \frac{x^3 - 1}{x - 1}$

📌 Nhận dạng: Dạng $\frac{0}{0}$

📌 Phân tích:

Sử dụng hằng đẳng thức:
$x^3 - 1 = (x - 1)(x^2 + x + 1)$

→ $\frac{(x - 1)(x^2 + x + 1)}{x - 1} = x^2 + x + 1$
⇒ $\lim_{x \to 1} x^2 + x + 1 = 1 + 1 + 1 = 3$

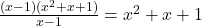
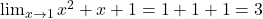
🐌 3. Giới hạn vô cực

Khi $x \to \infty $ hoặc \( x \to -\infty$ , ta xem hàm cư xử ra sao.

Ví dụ: $\lim_{x \to \infty} \frac{1}{x} = 0$

💬 Giải thích vui: Càng xa càng nhỏ – giống như bạn xa crush quá thì dần hết rung rinh 😅

Subscribe to get the latest posts sent to your email.

Leave a Reply Cancel reply