1. Nếu dãy hội tụ → có giới hạn
📉 Ví dụ: ![]()
➡️ Khi ![]() ,
, ![]()
🗨️ Giải thích vui: Hãy tưởng tượng một đứa trẻ bớt nghịch dần theo thời gian — càng lớn, càng ngoan → cuối cùng “ngoan hẳn” chính là giới hạn!
2. Dãy số tăng/giảm đơn điệu và bị chặn → hội tụ
🚦 Ví dụ: ![]()
➡️ Dãy tăng dần và luôn nhỏ hơn 1 → nên nó sẽ “tiến dần đến” 1 cuối cùng.
🗨️ Giải thích vui: Dãy này giống đứa trẻ leo cầu thang — leo đều và không được leo quá tầng cuối → kiểu gì cũng tới tầng cuối (giới hạn)!
3. Giới hạn vô cực
🌌 Ví dụ: ![]()
➡️ Khi ![]() ,
, ![]()
🗨️ Giải thích vui: Giống như lạm phát… cứ tăng hoài, chẳng có điểm dừng 😆
4. Quy tắc kẹp (Sandwich Rule)
🥪 Nếu ![]() , mà
, mà ![]() ,
, ![]() → thì
→ thì ![]()
🗨️ Giải thích vui: Giống như kẹp thịt giữa 2 lát bánh mì đã chín — thì miếng thịt kiểu gì cũng chín theo 😋
5. Giới hạn của tỉ số và căn
✂️ Nếu bạn có:
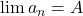 ,
, 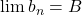 →
→ 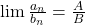 (trừ khi
(trừ khi 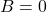 )
)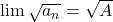 nếu
nếu 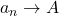 và
và 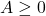
🗨️ Giải thích vui: Giống như bạn chia bánh cho bạn bè — nếu bánh ổn định, cách chia cũng ổn định!
6. Định lý giới hạn của dãy đặc biệt
🍕 Một vài “dãy VIP” đáng nhớ:
🗨️ Mấy dãy này là “người nổi tiếng” — ai học Toán cũng từng gặp!