Hệ số xác định — hay còn gọi là R bình phương (R²) — chính là “bài kiểm tra độ tin cậy” của mô hình hồi quy, kiểu như mô hình có làm tốt việc “đoán già đoán non” hay chỉ đoán… cho vui 😄
Hãy tưởng tượng bạn có một người bạn mê đoán số cân nặng của người khác. Nếu bạn ấy luôn đoán gần đúng, thì R² của bạn ấy cao gần bằng 1 — bạn có thể tin tưởng giao cả việc đoán giá tiền điện! Còn nếu bạn ấy đoán người gầy nặng 200kg và người lực lưỡng chỉ 45kg thì… R² tụt xuống sát đáy, và có lẽ bạn nên giữ lại công cụ tính của riêng mình 🫣
Nói nôm na:
- R² = 1 → Mô hình thần thánh, đoán như thần
- R² = 0 → Mô hình đoán mò, nên cho nghỉ
- R² < 0 → Mô hình tệ hơn cả trung bình cộng, đúng là… tự tin nhưng không đúng chỗ 😆
Thế nên mỗi khi R² lên cao, dân thống kê lại mở tiệc nhỏ ăn mừng. Còn khi nó rớt thảm, thì… đó là lúc nên xem lại cả bộ dữ liệu lẫn niềm tin vào mô hình 🧠📉
Cụ thể hơn, 
, hay hệ số xác định (Coefficient of Determination), là một chỉ số thống kê đo lường mức độ mô hình hồi quy giải thích được sự biến thiên của biến phụ thuộc (
) dựa trên biến độc lập (
).
Ý nghĩa
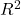- nằm trong khoảng từ 0 đến 1:
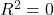: Mô hình không giải thích được sự thay đổi nào của biến phụ thuộc.
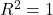: Mô hình giải thích hoàn toàn sự thay đổi của biến phụ thuộc.- Ví dụ:
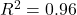nghĩa là 96% sự biến thiên của 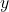được giải thích bởi 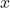, còn 4% do các yếu tố khác hoặc sai số.
Công thức
Trong đó:
SSR (Sum of Squared Residuals): Tổng bình phương sai số, tức là tổng bình phương chênh lệch giữa giá trị thực tế () và giá trị dự đoán (
).
SST (Total Sum of Squares): Tổng bình phương độ lệch của so với giá trị trung bình (
).
Ứng dụng trong ví dụ về Hồi quy tuyến tính đơn biến
Một công ty muốn phân tích xem chi phí quảng cáo (triệu đồng) ảnh hưởng thế nào đến doanh thu (triệu đồng). Dữ liệu lịch sử bao gồm chi phí quảng cáo (x) và doanh thu tương ứng (y).
Dữ liệu mẫu
| Chi phí quảng cáo (x) | Doanh thu (y) |
|---|---|
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 8 |
| 5 | 10 |
- Nếu 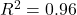, mô hình hồi quy tuyến tính
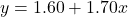giải thích 96% sự thay đổi của doanh thu dựa trên chi phí quảng cáo. - 4% còn lại có thể do các yếu tố khác (ví dụ: chất lượng sản phẩm, thị trường) hoặc sai số ngẫu nhiên.
