hồi quy đa thức - Cùng Học Cùng Mơ

Hãy tưởng tượng bạn đang ở một khu vui chơi, và nhiệm vụ của bạn là ném vòng vào các cột để giành giải thưởng. Nhưng thay vì ném vòng một cách ngẫu nhiên, bạn muốn tìm một đường cong “hoàn hảo” để vòng bay qua tất cả các cột một cách mượt mà nhất có thể. Hồi quy đa thức chính là công cụ giúp bạn vẽ ra đường cong đó! Nó không chỉ là một đường thẳng nhàm chán mà có thể uốn lượn, xoắn vặn như một chiếc tàu lượn siêu tốc, để mô tả dữ liệu của bạn một cách chính xác hơn.

Hãy nghĩ về hồi quy đa thức như một người nghệ sĩ vẽ tranh. Nếu hồi quy tuyến tính (linear regression) là một đứa trẻ chỉ biết vẽ đường thẳng bằng thước kẻ, thì hồi quy đa thức là một họa sĩ tài ba, có thể vẽ những đường cong mềm mại, phức tạp để “ôm” lấy các điểm dữ liệu của bạn.

Khi nào cần hồi quy đa thức?
Nếu dữ liệu của bạn không chịu nằm ngoan ngoãn trên một đường thẳng (như giá nhà tăng theo diện tích, nhưng có những lúc tăng vọt hoặc chững lại), hồi quy đa thức sẽ nhảy vào và nói: “Để tôi vẽ một đường cong cho bạn, bảo đảm đẹp!” Nó có thể mô tả các mối quan hệ phi tuyến (non-linear), như doanh thu bán kem tăng vọt vào mùa hè rồi giảm mạnh vào mùa đông.

Ví dụ vui:
Giả sử bạn muốn dự đoán số ly trà sữa bạn uống dựa trên số tiền trong ví. Nếu bạn càng giàu, bạn càng uống nhiều trà sữa, nhưng đến một mức nào đó, bạn “no” trà sữa và không uống thêm nữa. Một đường thẳng không thể mô tả được chuyện này, nhưng một đường cong (như parabol) thì có thể!

Hồi quy đa thức là một dạng mở rộng của hồi quy tuyến tính, được sử dụng để mô hình hóa mối quan hệ phi tuyến giữa biến độc lập $x$ và biến phụ thuộc $y$ . Thay vì tìm một đường thẳng $y = a + bx$ , hồi quy đa thức tìm một hàm đa thức bậc cao hơn, ví dụ:
$y = a + b_1x + b_2x^2 + b_3x^3 + \dots + b_nx^n ]Trong đó,$ latex n $là bậc của đa thức.   <h4 class="wp-block-heading"><strong>1. Công thức tổng quát</strong></h4>   Hàm hồi quy đa thức bậc$ latex n $có dạng:$ latex y = \beta_0 + \beta_1x + \beta_2x^2 + \beta_3x^3 + \dots + \beta_nx^n + \epsilon ]

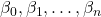$\beta_0, \beta_1, \dots, \beta_n$ : Các hệ số của đa thức (được ước lượng từ dữ liệu).
$\epsilon$ : Sai số ngẫu nhiên (phần dữ liệu không thể giải thích bởi mô hình).

Mặc dù hàm này trông “phi tuyến” (do các lũy thừa $x^2, x^3, \dots$ ), nó vẫn được giải bằng các phương pháp hồi quy tuyến tính. Bí mật nằm ở chỗ: ta biến các lũy thừa $x^2, x^3, \dots$ thành các biến mới, và vấn đề trở thành hồi quy tuyến tính đa biến.

2. Cách hoạt động

Để thực hiện hồi quy đa thức, ta làm các bước sau:

Chuyển đổi dữ liệu:
Biến đổi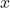 $x$ thành các lũy thừa của nó. Ví dụ, nếu bậc 2, ta tạo các cột dữ liệu mới: 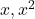$x, x^2$ . Nếu bậc 3, ta thêm $x^3$ .
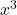Ví dụ:

Dữ liệu gốc: $(x_1, y_1), (x_2, y_2), \dots$
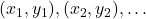
Với bậc 2, ta tạo ma trận: $[1, x_i, x_i^2]$ .

Ước lượng hệ số:
Sử dụng phương pháp bình phương tối thiểu (least squares) để tìm các hệ số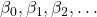 $\beta_0, \beta_1, \beta_2, \dots$ sao cho tổng bình phương sai số giữa giá trị dự đoán và giá trị thực tế là nhỏ nhất: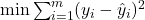
$\text{min} \sum_{i=1}^m (y_i - \hat{y}_i)^2 ]Trong đó,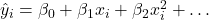$ latex \hat{y}_i = \beta_0 + \beta_1x_i + \beta_2x_i^2 + \dots $.</li>   <li><strong>Dự đoán</strong>:Sau khi có các hệ số, ta đưa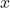$ latex x $vào hàm đa thức để dự đoán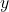$ latex y $.</li> </ol>   <h4 class="wp-block-heading"><strong>3. Khi nào dùng hồi quy đa thức?</strong></h4>   <ul class="wp-block-list"> <li>Dữ liệu có xu hướng phi tuyến (khi vẽ scatter plot, các điểm không nằm gần đường thẳng).</li>   <li>Bạn muốn mô hình hóa các mối quan hệ phức tạp, ví dụ: doanh thu theo thời gian, nhiệt độ theo độ cao, v.v.</li>   <li>Tuy nhiên, <strong>cẩn thận với bậc cao</strong>! 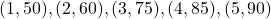Nếu bậc quá cao (overfitting), mô hình sẽ "học thuộc" dữ liệu, dẫn đến dự đoán kém trên dữ liệu mới.</li> </ul>   <h4 class="wp-block-heading"><strong>Ví dụ minh họa</strong></h4>   Giả sử bạn có dữ liệu về số giờ học ($ latex x $) và điểm thi ($ latex y $) của học sinh:   <ul class="wp-block-list"> <li>Dữ liệu:$ latex (1, 50), (2, 60), (3, 75), (4, 85), (5, 90) $.</li>   <li>Vẽ scatter plot, bạn thấy dữ liệu không thẳng mà hơi cong (như parabol).</li>   <li>Bạn thử hồi quy đa thức bậc 2:$ latex y = \beta_0 + \beta_1x + \beta_2x^2 ]
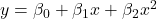
Sau khi tính toán (dùng thư viện như Python hoặc công cụ toán học), bạn tìm được:
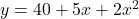
$y = 40 + 5x + 2x^2 ]</li>   <li>Giờ bạn có thể dự đoán: Nếu học 6 giờ, điểm thi sẽ là: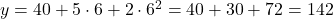$ latex y = 40 + 5 \cdot 6 + 2 \cdot 6^2 = 40 + 30 + 72 = 142 ] (tất nhiên, điểm tối đa thường là 100, nên cần kiểm tra lại!).

7. Lưu ý quan trọng

Chọn bậc đa thức: Dùng cross-validation để kiểm tra bậc nào tốt nhất (thường bậc 2 hoặc 3 là đủ cho nhiều bài toán).
Chuẩn hóa dữ liệu: Nếu $x$ có giá trị lớn, $x^2, x^3$ sẽ rất lớn, gây khó khăn cho tính toán. Hãy chuẩn hóa dữ liệu trước.
So sánh với các mô hình khác: Nếu hồi quy đa thức không hiệu quả, thử các mô hình phi tuyến khác (như hồi quy kernel, cây quyết định, hoặc mạng nơ-ron).

Kiểm tra mô hình trên dữ liệu mới (dữ liệu kiểm tra) để chắc chắn nó không “ảo tưởng sức mạnh”.

6. Cách thực hiện trong thực tế

Trong Python, bạn có thể dùng thư viện scikit-learn để thực hiện hồi quy đa thức:

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline

# Tạo pipeline cho hồi quy đa thức bậc 2
polyreg = make_pipeline(PolynomialFeatures(degree=2), LinearRegression())

# Huấn luyện mô hình
polyreg.fit(X_train.reshape(-1, 1), y_train)

# Dự đoán
y_pred = polyreg.predict(X_test.reshape(-1, 1))

Ưu điểm và nhược điểm

Ưu điểm:

Linh hoạt, có thể mô tả các mối quan hệ phi tuyến.
Dễ triển khai (vẫn dựa trên hồi quy tuyến tính).
Phù hợp với nhiều bài toán thực tế.

Nhược điểm:
Overfitting: Nếu chọn bậc đa thức quá cao, mô hình sẽ quá phức tạp và không tổng quát hóa tốt.
Tốn tài nguyên: Khi bậc đa thức tăng, số lượng biến tăng theo, dẫn đến tính toán phức tạp hơn.
Không ổn định ở biên: Đa thức bậc cao có thể dao động mạnh ở các giá trị $x$ ngoài phạm vi dữ liệu.

2. Cách hoạt động

7. Lưu ý quan trọng

6. Cách thực hiện trong thực tế

Ưu điểm và nhược điểm

Related Posts

Để lại một bình luận Hủy