Phân phối Bernoulli và Ứng Dụng Thực Tế

Phân phối Bernoulli là một phân phối xác suất rời rạc mô tả kết quả của một thí nghiệm chỉ có hai khả năng xảy ra: thành công (ký hiệu là 1) hoặc thất bại (ký hiệu là 0). Phân phối này được đặt theo tên nhà toán học Thụy Sĩ Jacob Bernoulli.

Đặc điểm của phân phối Bernoulli:

• Hai kết quả: Chỉ có hai kết quả có thể xảy ra: 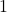(thành công) hoặc 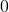(thất bại).
• Xác suất:
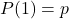• , trong đó 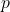là xác suất thành công.
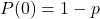• , trong đó là xác suất thất bại.
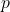• : phải là một giá trị trong khoảng từ 0 đến 1.

Hàm xác suất của phân phối Bernoulli:

Hàm xác suất của biến ngẫu nhiên Bernoulli được định nghĩa như sau: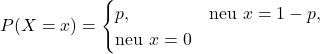

Trong đó là xác suất thành công.

Các tham số quan trọng:

1. Kỳ vọng (giá trị trung bình):
   
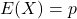
   Kỳ vọng của một phân phối Bernoulli là xác suất thành công \)p\).
2. Phương sai:
   
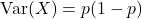
   Phương sai đo lường mức độ phân tán của các giá trị quanh kỳ vọng.

Ví dụ về phân phối Bernoulli:

• Tung một đồng xu:
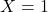• nếu là mặt sấp, và 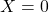nếu là mặt ngửa.
• Nếu đồng xu là cân bằng, xác suất mặt sấp là 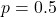, và xác suất mặt ngửa là .
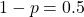• Trong một bài kiểm tra trắc nghiệm với một câu hỏi, nếu chọn ngẫu nhiên một đáp án, 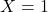nếu trả lời đúng và 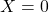nếu trả lời sai.

Ứng dụng:

Phân phối Bernoulli thường được sử dụng trong các thí nghiệm chỉ có hai kết quả, như trong thử nghiệm lâm sàng (kết quả điều trị thành công hoặc thất bại), hoặc kiểm tra sản phẩm đạt hay không đạt chất lượng.

Phân phối Bernoulli cũng là cơ sở để xây dựng các phân phối khác phức tạp hơn như phân phối nhị thức (binomial distribution), trong đó kết quả của nhiều thí nghiệm Bernoulli độc lập được cộng dồn.

///

chi tiết hơn:

Khái Niệm Cơ Bản Về Phân Phối Bernoulli

Phân phối Bernoulli là một trong những khái niệm cơ bản nhất trong lý thuyết xác suất, được sử dụng để mô tả các thử nghiệm chỉ có hai kết quả: thành công hoặc thất bại. Định nghĩa chính xác của phân phối Bernoulli là một hàm xác suất mà ở đó biến ngẫu nhiên chỉ có hai giá trị: 1 (thành công) và 0 (thất bại). Biến ngẫu nhiên này thường được ký hiệu là X, với xác suất thành công được ký hiệu là p, và xác suất thất bại là 1 – p. Đây chính là các thông số cơ bản của phân phối này.

Các tính chất chính của phân phối Bernoulli bao gồm tỷ lệ thành công, kỳ vọng và phương sai. Tỷ lệ thành công p, là mức độ khả năng xảy ra của trường hợp thành công trong thử nghiệm. Kỳ vọng của một phân phối Bernoulli được tính bằng công thức E(X) = p, cho thấy giá trị trung bình của biến ngẫu nhiên. Đối với phương sai, nó được tính bằng Var(X) = p(1 – p), phản ánh mức độ biến thiên của các kết quả trong thử nghiệm.

Để làm rõ hơn khái niệm này, có thể xem xét ví dụ đơn giản như việc tung một đồng xu. Nếu một đồng xu công bằng được tung lên, xác suất để nó rơi vào mặt sấp (thành công) là 0.5 và mặt ngửa (thất bại) cũng là 0.5. Trong trường hợp này, biến ngẫu nhiên X có thể nhận giá trị 1 (mặt sấp) với xác suất p = 0.5, và giá trị 0 (mặt ngửa) với xác suất 1 – p = 0.5. Phân phối Bernoulli không chỉ là nền tảng cho nhiều phân phối phức tạp hơn như phân phối nhị thức mà còn là công cụ quan trọng trong lĩnh vực thống kê và xác suất.

Các Tính Chất Của Phân Phối Bernoulli

Phân phối Bernoulli là một trong những phân phối xác suất cơ bản nhất trong lý thuyết xác suất và thống kê. Nó mô tả kết quả của một thí nghiệm mà chỉ có hai kết quả có thể xảy ra: thành công (thường được ký hiệu là 1) và thất bại (ký hiệu là 0). Một trong những đặc điểm quan trọng của phân phối này là kỳ vọng (expected value) và phương sai (variance), hai chỉ số này cung cấp sự hiểu biết sâu sắc về bản chất của các sự kiện xảy ra trong mô hình Bernoulli.

Kỳ vọng của một biến ngẫu nhiên theo phân phối Bernoulli được tính bằng công thức: E(X) = p, trong đó p là xác suất của thành công. Điều này có nghĩa là kỳ vọng cho biết tần suất trung bình mà một sự kiện thành công xảy ra trong một loạt các lần thử. Ví dụ, nếu chúng ta xác định rằng xác suất ra một sản phẩm đạt yêu cầu là 0.8, tức là 80%, thì kỳ vọng cho số sản phẩm đạt yêu cầu trong 100 lần thử sẽ là 80 sản phẩm. Điều này chứng minh rằng kỳ vọng không chỉ có giá trị lý thuyết mà còn rất khả thi khi áp dụng vào thực tiễn.

Phương sai được định nghĩa là Var(X) = p(1-p). Phương sai cung cấp thông tin về sự phân tán của các kết quả quanh giá trị kỳ vọng. Nếu xác suất thành công p càng lớn hoặc càng nhỏ, phương sai sẽ giảm, cho thấy rằng kết quả thực tế sẽ ngày càng gần với kỳ vọng. Ngược lại, khi p tiến gần đến 0.5, phương sai cao hơn, điều này cho thấy sự phân tán lớn hơn giữa các kết quả. Qua đó, các tính chất của phân phối Bernoulli không chỉ giúp hiểu rõ hơn về tổng thể mà còn cung cấp những ứng dụng thực tiễn trong nhiều lĩnh vực, từ kinh doanh đến khoa học.

Ứng Dụng Thực Tế Của Phân Phối Bernoulli

Phân phối Bernoulli, một trong những phân phối xác suất cơ bản nhất, mang lại nhiều ứng dụng hữu ích trong nhiều lĩnh vực khác nhau như kinh tế, y tế và nghiên cứu thị trường. Một trong những ứng dụng nổi bật nhất của phân phối này là trong việc đánh giá rủi ro trong các quyết định đầu tư. Cụ thể, nhà đầu tư có thể sử dụng phân phối Bernoulli để mô phỏng khả năng thành công hoặc thất bại của một dự án đầu tư, giúp họ đưa ra quyết định tài chính chính xác hơn.

Trong lĩnh vực y tế, phân phối Bernoulli thường được áp dụng để đánh giá tình trạng sức khỏe của bệnh nhân. Ví dụ, khi xem xét một phương pháp điều trị mới, các nhà nghiên cứu có thể sử dụng phân phối Bernoulli để xác định tỷ lệ bệnh nhân đáp ứng tích cực với điều trị so với những người không có phản ứng. Điều này giúp họ đưa ra kết luận về hiệu quả của phương pháp điều trị trong một nhóm bệnh nhân.

Hơn nữa, trong nghiên cứu thị trường, doanh nghiệp có thể tận dụng phân phối Bernoulli để phân tích hành vi của khách hàng. Chẳng hạn, khi khảo sát quan điểm của khách hàng về một sản phẩm mới, các công ty có thể thu thập dữ liệu về việc khách hàng có mua sản phẩm hay không. Sử dụng phân phối này, doanh nghiệp có thể ước tính xác suất để khách hàng thực hiện giao dịch, từ đó điều chỉnh chiến lược tiếp thị cho phù hợp.

Như vậy, phân phối Bernoulli không chỉ có giá trị lý thuyết mà còn áp dụng rộng rãi trong thực tế, giúp các nhà nghiên cứu và nhà phân tích đưa ra quyết định chính xác dựa trên dữ liệu. Sự linh hoạt và tính ứng dụng cao của nó trong nhiều lĩnh vực chứng tỏ rằng phân phối Bernoulli là một công cụ rất hữu ích trong công việc hàng ngày và trong việc thực hiện các nghiên cứu khoa học.

So sánh với các phân phối khác

Phân phối Bernoulli là một trong những mô hình xác suất cơ bản, có thể được so sánh với nhiều phân phối khác như phân phối nhị thức và phân phối Poisson. Để hiểu rõ hơn về vị trí của phân phối Bernoulli trong lý thuyết xác suất, trước tiên, cần xem xét cách mà các phân phối này khác nhau về mặt tính chất cũng như ứng dụng.

Phân phối nhị thức, được xây dựng từ nhiều thử nghiệm Bernoulli độc lập, mô tả số thành công trong n thử nghiệm đơn giản. Đây là một phân phối có thể được coi là sự mở rộng trực tiếp của phân phối Bernoulli khi có nhiều hơn một thử nghiệm. Ví dụ, nếu chúng ta đang nghiên cứu lượng phiếu bầu cho hai ứng cử viên trong một cuộc bầu cử, phân phối nhị thức sẽ hữu ích hơn để tính toán xác suất có bao nhiêu phiếu bầu cho một ứng cử viên cụ thể, trong khi phân phối Bernoulli chỉ cho phép tính xác suất cho một lần phiếu bầu.

Phân phối Poisson, trong khi đó, được sử dụng để mô hình các sự kiện ngẫu nhiên xảy ra trong một khoảng thời gian nhất định, với điều kiện sự kiện đó xảy ra độc lập và với tỷ lệ không đổi. Phân phối này có thể là một lựa chọn tốt để phân tích số lượng sự cố trong một khoảng thời gian nhất định, ví dụ như số lượng cuộc gọi đến một tổng đài trong một giờ.

Tóm lại, phân phối Bernoulli thường được sử dụng trong các trường hợp đơn giản với kết quả nhị phân, trong khi đó phân phối nhị thức và Poisson thích hợp cho những bài toán phức tạp hơn trong việc phân tích sự kiện nhiều lần hoặc trong khoảng thời gian dài. Khi chọn loại phân phối nào để áp dụng, người dùng nên xem xét cẩn thận bản chất của dữ liệu và câu hỏi nghiên cứu của mình.