Phân phối chuẩn nhiều chiều (multivariate normal distribution)

Phân phối chuẩn nhiều chiều là gì?

Hãy tưởng tượng bạn đang tổ chức một bữa tiệc pizza 🍕 cho một nhóm bạn. Mỗi người có hai sở thích chính: thích ăn pizza mặn (như pepperoni) và thích ăn pizza ngọt (như pizza Nutella). Nếu bạn vẽ sở thích của mọi người lên một biểu đồ, mỗi người sẽ là một điểm trên mặt phẳng, với trục X là “mức độ thích pizza mặn” và trục Y là “mức độ thích pizza ngọt”.

Bây giờ, nếu sở thích của mọi người có xu hướng tập trung quanh một điểm trung bình (ví dụ: đa số thích mặn vừa vừa và ngọt vừa vừa), và các điểm này lan tỏa ra xung quanh theo một hình dạng elip đẹp đẽ, thì đó chính là hình ảnh của phân phối chuẩn nhiều chiều! 🎉

Tải ảnh

Phân phối chuẩn nhiều chiều là phiên bản “xịn” hơn của phân phối chuẩn một chiều (hình chuông 🔔 quen thuộc). Thay vì chỉ xét một đặc tính (như chiều cao), nó xét nhiều đặc tính cùng lúc (như chiều cao, cân nặng, IQ) và mô tả cách các đặc tính này phân bố chung với nhau.

Hàm mật độ của phân phối chuẩn nhiều chiều

Hàm mật độ (probability density function – PDF) của phân phối chuẩn nhiều chiều giống như một công thức “nấu ăn” để tính xác suất bạn tìm thấy một người với tổ hợp sở thích cụ thể trong bữa tiệc pizza của mình. Công thức này trông hơi “hầm hố”, nhưng mình sẽ giải thích nó một cách vui vẻ:

Công thức hàm mật độ

Hàm mật độ của phân phối chuẩn nhiều chiều cho một vector $\mathbf{x}$ (ví dụ: $\mathbf{x} = [x_1, x_2]$ là sở thích mặn và ngọt) được viết như sau:

$f(\mathbf{x}) = \frac{1}{(2\pi)^{k/2} |\Sigma|^{1/2}} \exp\left(-\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{x} - \boldsymbol{\mu})\right)$

Đừng sợ! 😅 Hãy chia nhỏ công thức này ra như cách bạn cắt một cái pizza:

$\mathbf{x}$ : Đây là điểm bạn đang xét, ví dụ: sở thích của một người ([mặn, ngọt]).
$\boldsymbol{\mu}$ : Vector trung bình, tức là điểm trung tâm của đám đông. Ví dụ: trung bình mọi người thích 5/10 điểm mặn và 4/10 điểm ngọt.
$\Sigma$ : Ma trận hiệp phương sai (covariance matrix), nó nói cho bạn đám đông “lan tỏa” thế nào. Nếu mọi người có sở thích rất giống nhau, elip sẽ hẹp. Nếu sở thích đa dạng, elip sẽ rộng. Nó cũng cho biết liệu sở thích mặn và ngọt có tương quan không (ví dụ: ai thích mặn nhiều thì có thích ngọt ít không?).
$|\Sigma|$ : Định thức của ma trận hiệp phương sai, giúp chuẩn hóa để hàm mật độ có tổng xác suất bằng 1.
$\Sigma^{-1}$ : Ma trận nghịch đảo của $\Sigma$ , giúp đo khoảng cách từ $\mathbf{x}$ đến trung bình $\boldsymbol{\mu}$ theo cách “cong cong” của elip.
$\exp(\cdot)$ : Phần này tạo ra hình chuông, làm cho xác suất giảm dần khi bạn đi xa trung bình.
$(2\pi)^{k/2}$ : Một hằng số để đảm bảo hàm mật độ hợp lệ, với $k$ là số chiều (ví dụ: 2 chiều cho mặn và ngọt).

Cách nhớ hàm mật độ

Để nhớ công thức này mà không đau đầu, hãy nghĩ nó như một câu chuyện:

Câu chuyện về bữa tiệc pizza:

Tưởng tượng bạn đứng ở trung tâm bữa tiệc ( $\boldsymbol{\mu}$ ).
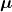Bạn muốn biết xác suất một người có sở thích cụ thể ( $\mathbf{x}$ ) xuất hiện.
Khoảng cách từ người đó đến bạn được đo bằng khoảng cách Mahalanobis 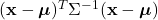$(\mathbf{x} - \boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{x} - \boldsymbol{\mu})$ , tức là khoảng cách “cong” theo hình dạng elip của đám đông.
Nếu người đó ở gần trung tâm, xác suất cao (hàm mật độ lớn). Nếu họ ở xa (thích pizza siêu mặn hoặc siêu ngọt), xác suất thấp.

Mẹo nhớ công thức:
Phần chuẩn hóa (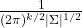 $\frac{1}{(2\pi)^{k/2} |\Sigma|^{1/2}}$ ): Đây là “bánh pizza nền”, đảm bảo tổng xác suất bằng 1. Nghĩ đến việc cắt bánh pizza thành các phần đều nhau.
Phần lũy thừa (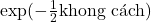 $\exp(-\frac{1}{2} \text{khoảng cách})$ ): Đây là “phô mai tan chảy”, tạo ra hình chuông mềm mại, nơi xác suất giảm dần khi đi xa trung tâm.
Ma trận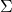 $\Sigma$ : Nghĩ nó như “hình dạng của đám đông”. Nếu đám đông đứng thành vòng tròn, 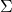$\Sigma$ đơn giản. Nếu đám đông kéo dài thành elip, 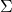$\Sigma$ phức tạp hơn.
Ví dụ trực quan:

Nếu bạn vẽ hàm mật độ trên không gian 2D, nó sẽ tạo ra một đồi chuông 3D với đỉnh ở 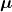$\boldsymbol{\mu}$ . Độ cao của đồi tại một điểm $\mathbf{x}$ chính là xác suất mật độ tại đó.
Nếu bạn cắt ngang đồi, bạn sẽ thấy các đường đồng mức (contour) hình elip, đại diện cho các vùng có xác suất tương đương.

Tóm lại

Phân phối chuẩn nhiều chiều giống như một “đám mây elip” mô tả cách các đặc tính (như sở thích pizza) phân bố cùng nhau. Hàm mật độ là công thức để tính xác suất tại một điểm trong đám mây đó. Để nhớ, hãy nghĩ về một bữa tiệc pizza với đám đông tụ tập quanh sở thích trung bình, và công thức là cách bạn đo lường “mức độ đông đúc” tại một điểm! 😄

Code Python và R để vẽ đồ thị cho phân phối chuẩn 2 chiều (bivariate normal distribution)

3D surface plot

# Nhập thư viện cần thiết
import numpy as np                      # Xử lý mảng số học
import matplotlib.pyplot as plt         # Vẽ đồ thị
from scipy.stats import multivariate_normal  # Phân phối chuẩn đa biến

# Tạo lưới điểm và khai báo phân phối chuẩn hai biến
mean = [0, 0]                     # Trung bình của hai biến
cov = [[1, 0.5], [0.5, 1]]        # Ma trận hiệp phương sai (mức độ tương quan)

x = np.linspace(-3, 3, 100)       # Tạo dãy giá trị cho trục X
y = np.linspace(-3, 3, 100)       # Tạo dãy giá trị cho trục Y
X, Y = np.meshgrid(x, y)          # Tạo lưới 2D từ X và Y
pos = np.dstack((X, Y))           # Ghép X và Y thành mảng tọa độ điểm

rv = multivariate_normal(mean, cov)   # Khai báo phân phối
Z = rv.pdf(pos)                       # Tính mật độ xác suất tại mỗi điểm

# Vẽ biểu đồ bề mặt 3D
fig = plt.figure(figsize=(8,6))       # Tạo khung hình
ax = fig.add_subplot(111, projection='3d')  # Khởi tạo đồ thị 3D
ax.plot_surface(X, Y, Z, cmap='viridis', linewidth=0, antialiased=False)  # Vẽ bề mặt

# Gán nhãn cho các trục và tiêu đề
ax.set_xlabel('X')               # Nhãn trục X
ax.set_ylabel('Y')               # Nhãn trục Y
ax.set_zlabel('Mật độ xác suất') # Nhãn trục Z
plt.title('Phân phối chuẩn hai biến')  # Tiêu đề biểu đồ
plt.show()                        # Hiển thị biểu đồ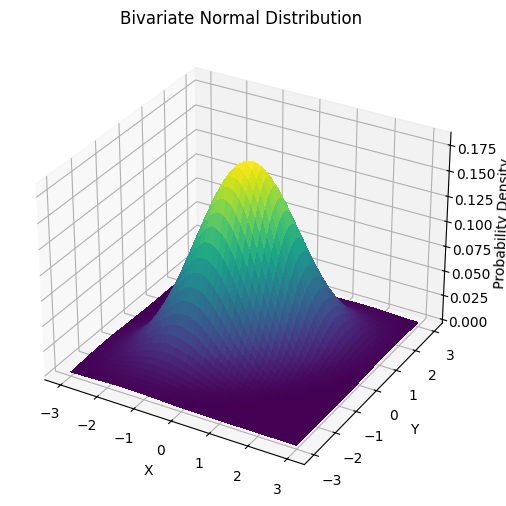

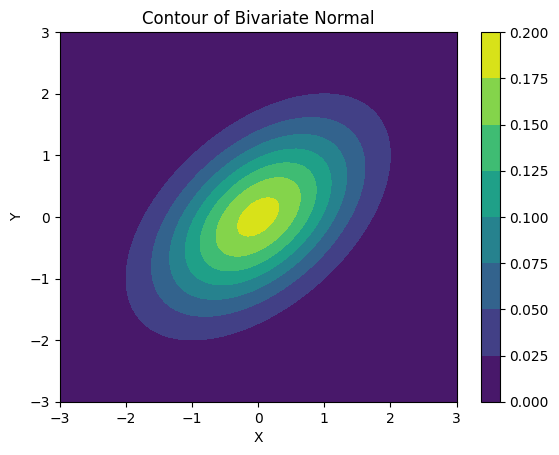
Tải ảnh

Vẽ các dải màu biểu thị mật độ xác suất

# Vẽ các dải màu biểu thị mật độ xác suất
plt.contourf(X, Y, Z, cmap='viridis')  
plt.xlabel('X')                        # Gán nhãn cho trục X
plt.ylabel('Y')                        # Gán nhãn cho trục Y
plt.title('Contour of Bivariate Normal')  # Tiêu đề biểu đồ
# Hiển thị thanh màu (giải thích màu sắc theo giá trị)
plt.colorbar()                         
plt.show()                             # Hiển thị biểu đồ

Chạy trên Colab

kết quả

Code R

%%R
# Cài đặt các gói cần thiết
install.packages("mvtnorm")    # Phân phối chuẩn đa biến
install.packages("plotly")     # Vẽ đồ thị 3D tương tác

# Tải thư viện cần thiết
library(mvtnorm)
library(ggplot2)
library(plotly)

# Tạo lưới điểm và tính mật độ
x <- seq(-3, 3, length.out = 100)  # Tạo dãy giá trị cho trục X
y <- seq(-3, 3, length.out = 100)  # Tạo dãy giá trị cho trục Y
grid <- expand.grid(X = x, Y = y) # Tạo lưới 2D từ X và Y

mean <- c(0, 0)  # Trung bình của hai biến
sigma <- matrix(c(1, 0.6, 0.6, 1), nrow = 2)  # Ma trận hiệp phương sai

grid$Z <- dmvnorm(grid, mean = mean, sigma = sigma)  # Tính mật độ tại mỗi điểm trong lưới

# Vẽ đồ thị đường đồng mức (contour)
ggplot(grid, aes(x = X, y = Y, z = Z)) +
  geom_contour_filled() +
  labs(title = "Phân phối chuẩn hai biến", x = "X", y = "Y") +
  theme_minimal()