Quy tắc L’Hôpital là như gọi “bác sĩ toán học” tới để chữa những ca giới hạn gặp tai nạn – đặc biệt là các dạng vô định như ![]() hoặc
hoặc ![]() .
.
🧠 Cách hoạt động của quy tắc L’Hôpital
🔧 Nguyên lý:
Khi một giới hạn có dạng vô định:
![]()
→ Thì ta có thể chuyển sang đạo hàm:
![]()
Miễn là
🌈 Vì sao quy tắc này “hợp lý”?
- Đạo hàm phản ánh tốc độ thay đổi
Khi tử và mẫu đều tiệm cận về 0 hoặc vô cực, ta không biết “ai mạnh hơn” → dùng đạo hàm để xem ai tăng/giảm nhanh hơn! - Giới hạn ban đầu quá “mù mờ”
Dạng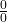 giống như chia hai bóng ma – dùng đạo hàm để “soi ánh sáng” sự biến thiên của chúng.
giống như chia hai bóng ma – dùng đạo hàm để “soi ánh sáng” sự biến thiên của chúng. - Tư duy tỉ số tốc độ
Nếu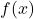 và
và 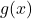 đều tiến về 0, thì tỉ số
đều tiến về 0, thì tỉ số 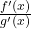 cho biết ai “rớt xuống” nhanh hơn → từ đó suy ra giới hạn chính xác.
cho biết ai “rớt xuống” nhanh hơn → từ đó suy ra giới hạn chính xác.
Tưởng tượng bạn và người bạn cùng chạy đua:
Cả hai bắt đầu đứng yên tại vạch xuất phát (giá trị bằng 0) – nhưng khi tính giới hạn, ta cần biết ai tăng tốc nhanh hơn!
→ Đạo hàm giống như đồng hồ tốc độ → Ai chạy nhanh hơn sẽ “thắng trong giới hạn”! 🏁🏃
Ví dụ 1
Thật vậy, dùng quy tắc L’Hôpital:
- Đạo hàm tử:
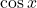
- Đạo hàm mẫu:
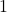
⇒![Rendered by QuickLaTeX.com \[\lim_{x \to 0} \frac{\sin x}{x} = \lim_{x \to 0} \frac{\cos x}{1} = 1\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-b1f31f7a09803a7e15adb89240f61429_l3.png)
Nếu bạn vẽ đồ thị sin(x) và x gần x = 0, đường cong của sin(x) gần như trùng khít với đường thẳng y = x → tỉ lệ của chúng là 1
Cách hiểu đơn giản:
Khi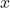 tiến về 0, cả sin(x) và x đều gần như giống nhau → tỉ lệ giữa chúng tiến về 1.
tiến về 0, cả sin(x) và x đều gần như giống nhau → tỉ lệ giữa chúng tiến về 1.
Nói cách khác, khi x rất nhỏ, sin(x) ≈ x
💉 Ví dụ 2: Dạng 0/0 cổ điển
Tính:
![]()
📌 Nhận dạng:
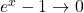 ,
, 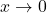 → dạng
→ dạng 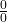
📌 Áp dụng L’Hôpital:- Tử: đạo hàm
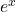
- Mẫu: đạo hàm
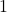
→![Rendered by QuickLaTeX.com \[\lim_{x \to 0} \frac{e^x}{1} = 1\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-2ef83e6a219d67c91ddd8b2ecf8f586f_l3.png)
⚡ Ví dụ 3: Dạng vô cực / vô cực “đấu tay đôi”
Tính:
![]()
📌 Dạng:
📌 Áp dụng L’Hôpital:
- Tử:
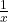 , Mẫu:
, Mẫu: 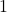
→![Rendered by QuickLaTeX.com \[\lim_{x \to \infty} \frac{1/x}{1} = 0\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-b08bfa4a3534413aa00f549f70087122_l3.png)
💉 Ví dụ 4:
Tính giới hạn:
![]()
🔍 Bước 1: Nhận dạng dạng vô định
Thay trực tiếp ![]() :
:
- Tử số:
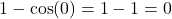
- Mẫu số:
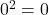
→ Dạng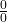 → đủ điều kiện dùng L’Hôpital
→ đủ điều kiện dùng L’Hôpital
🧪 Bước 2: Đạo hàm tử và mẫu
- Đạo hàm tử:
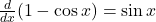
- Đạo hàm mẫu:
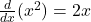
⇒ Giới hạn mới:
![]()
🔬 Bước 3: Đạo hàm thêm lần nữa
Lại thay ![]() :
:
→ Vẫn là ![]() → dùng tiếp L’Hôpital lần 2:
→ dùng tiếp L’Hôpital lần 2:
- Đạo hàm tử:
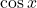
- Đạo hàm mẫu:
⇒ Giới hạn mới:
![]()
✅ Kết quả:
![]()