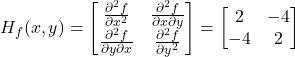Ví dụ về ma trận Hessian (Hessian matrix)

ma trận Hessian (Hessian matrix) là ma trận chứa tất cả các đạo hàm bậc hai của một hàm số đa biến.

Cho hàm số thực $f: \mathbb{R}^n \to \mathbb{R}$ có đạo hàm bậc hai liên tục, ma trận Hessian của $f$ tại điểm $\mathbf{x} = (x_1, x_2, …, x_n)$ là ma trận vuông kích thước $n \times n$ như sau:

$H_f(\mathbf{x}) =\begin{bmatrix}\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\\vdots & \vdots & \ddots & \vdots \\\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2}\end{bmatrix}$

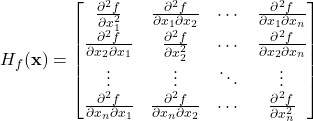
Ví dụ minh họa

Xét hàm số hai biến:

$f(x,y) = x^3 y + 2xy^2 + y^3$

Bước 1: Tính các đạo hàm bậc nhất:

$\frac{\partial f}{\partial x} = 3x^2 y + 2 y^2$

$\frac{\partial f}{\partial y} = x^3 + 4xy + 3y^2$

Bước 2: Tính các đạo hàm bậc hai:

$\frac{\partial^2 f}{\partial x^2} = \frac{\partial}{\partial x} (3x^2 y + 2 y^2) = 6xy + 0 = 6xy$

$\frac{\partial^2 f}{\partial y^2} = \frac{\partial}{\partial y} (x^3 + 4xy + 3y^2) = 0 + 4x + 6y = 4x + 6y$

$\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial}{\partial y} (3x^2 y + 2 y^2) = 3x^2 + 4y$

$\frac{\partial^2 f}{\partial y \partial x} = \frac{\partial}{\partial x} (x^3 + 4xy + 3y^2) = 3x^2 + 4y$

Vậy ma trận Hessian là:

$H_f(x,y) =\begin{bmatrix}6xy & 3x^2 + 4y \\3x^2 + 4y & 4x + 6y\end{bmatrix}$

Ví dụ 2:

Xét hàm số:

$f(x, y) = x^2 - 4xy + y^2$

Bước 1: Tính đạo hàm riêng bậc nhất

$\frac{\partial f}{\partial x} = 2x - 4y$

$\frac{\partial f}{\partial y} = -4x + 2y$

Bước 2: Tính các đạo hàm riêng bậc hai

$\frac{\partial^2 f}{\partial x^2} = 2\quad ; \quad\frac{\partial^2 f}{\partial y^2} = 2$

$\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x} = -4$

Ma trận Hessian:

$H_f(x, y) =\begin{bmatrix}\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}\end{bmatrix}=\begin{bmatrix}2 & -4 \\-4 & 2\end{bmatrix}$

Ví dụ minh họa

Ví dụ 2:

Related Posts

Để lại một bình luận Hủy