Ví dụ về tính ma trận Jacobian

Spread the love

📌 Ma trận Jacobian là gì?

Ma trận Jacobian là ma trận chứa các đạo hàm riêng của từng thành phần của hàm véc-tơ theo từng biến.

$J_{\mathbf{F}}(x, y) =\begin{bmatrix}\frac{\partial f_1}{\partial x} & \frac{\partial f_1}{\partial y} \\\frac{\partial f_2}{\partial x} & \frac{\partial f_2}{\partial y}\end{bmatrix}$

🧮 Ví dụ:

Xét hàm véc-tơ:

$\mathbf{F}(x, y) =\begin{bmatrix}f_1(x, y) \\f_2(x, y)\end{bmatrix}\begin{bmatrix}x^2 y + \sin(y) \\e^x + xy\end{bmatrix}$

Mục tiêu:

Tính ma trận Jacobian của hàm $\mathbf{F}(x, y)$ .

🔍 Tính từng đạo hàm:

Với $f_1(x, y) = x^2 y + \sin(y)$

$\frac{\partial f_1}{\partial x} = 2x y$
$\frac{\partial f_1}{\partial y} = x^2 + \cos(y)$

Với $f_2(x, y) = e^x + xy$

$\frac{\partial f_2}{\partial x} = e^x + y$
$\frac{\partial f_2}{\partial y} = x$

✅ Ma trận Jacobian thu được:

$J_{\mathbf{F}}(x, y) =\begin{bmatrix}2xy & x^2 + \cos(y) \\e^x + y & x\end{bmatrix}$

🧮 Ví dụ 2:

Xét hàm véc-tơ: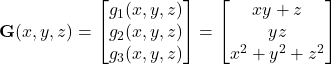
$\mathbf{G}(x, y, z) =\begin{bmatrix}g_1(x, y, z) \\g_2(x, y, z) \\g_3(x, y, z)\end{bmatrix}=\begin{bmatrix}xy + z \\yz \\x^2 + y^2 + z^2\end{bmatrix}$

Mục tiêu:

Tính ma trận Jacobian của $\mathbf{G}(x, y, z)$ .

🔍 Công thức tổng quát ma trận Jacobian:

$J_{\mathbf{G}}(x, y, z) =\begin{bmatrix}\frac{\partial g_1}{\partial x} & \frac{\partial g_1}{\partial y} & \frac{\partial g_1}{\partial z} \\\frac{\partial g_2}{\partial x} & \frac{\partial g_2}{\partial y} & \frac{\partial g_2}{\partial z} \\\frac{\partial g_3}{\partial x} & \frac{\partial g_3}{\partial y} & \frac{\partial g_3}{\partial z}\end{bmatrix}$

🧠 Tính các đạo hàm riêng:

Với $g_1(x, y, z) = xy + z$ :

$\frac{\partial g_1}{\partial x} = y,\quad\frac{\partial g_1}{\partial y} = x,\quad\frac{\partial g_1}{\partial z} = 1$

Với $g_2(x, y, z) = yz$ :

$\frac{\partial g_2}{\partial x} = 0,\quad\frac{\partial g_2}{\partial y} = z,\quad\frac{\partial g_2}{\partial z} = y$

Với $g_3(x, y, z) = x^2 + y^2 + z^2$ :

$\frac{\partial g_3}{\partial x} = 2x,\quad\frac{\partial g_3}{\partial y} = 2y,\quad\frac{\partial g_3}{\partial z} = 2z$

✅ Ma trận Jacobian cuối cùng:

$J_{\mathbf{G}}(x, y, z) =\begin{bmatrix}y & x & 1 \\0 & z & y \\2x & 2y & 2z\end{bmatrix}$

Discover more from Cùng Học Cùng Mơ

Subscribe to get the latest posts sent to your email.