Trong toán học, giới hạn một bên là khi bạn xét hành vi của một hàm số khi biến số tiến đến một điểm nào đó, nhưng chỉ từ một phía – bên trái hoặc bên phải.
Nhưng để dễ hình dung hơn, tưởng tượng bạn đang đi đến nhà người bạn tên là “Điểm A”. Có hai con đường:
- Một con đường đi từ bên trái (ví dụ từ số 0.9 đến gần 1).
- Một con đường đi từ bên phải (ví dụ từ số 1.1 về gần 1).
Bạn đang tự hỏi: “Không biết đi từ phía nào thì cảnh vật, không khí, cảm giác… có giống nhau không ta?”
Toán học cũng hỏi y như vậy! Và đó chính là lý do chúng ta có khái niệm:
✏️ Định nghĩa:
✅ Giới hạn bên trái:
Nếu ![]() tiến đến một giá trị
tiến đến một giá trị ![]() khi
khi ![]() từ phía nhỏ hơn (bên trái), ta viết:
từ phía nhỏ hơn (bên trái), ta viết:
![]()
✅ Giới hạn bên phải:
Nếu ![]() khi
khi ![]() từ phía lớn hơn (bên phải), ta viết:
từ phía lớn hơn (bên phải), ta viết:
![]()
👉 Nếu hai giới hạn một bên bằng nhau, thì ta nói giới hạn “hai bên” tại điểm đó tồn tại.
🎉 Ví dụ:
Hãy tưởng tượng có một tiệm cà phê tên là “Hàm Số” với bảng giá như sau:
☕ Trước 12h trưa: 20k
☕ Sau 12h trưa: 30k
Giờ thử xét xem chuyện gì xảy ra tại đúng 12h:
- Từ sáng sớm đi đến 12h (giới hạn trái): cà phê còn 20k.
- Từ chiều quay lại gần 12h (giới hạn phải): cà phê đã 30k.
⛔ Kết luận:
![]()
Vì hai giá trị này khác nhau, nên giới hạn tại 12h không tồn tại!
Giới hạn một bên (hay giới hạn một phía) trong toán học là giới hạn khi biến số tiến tới một giá trị nào đó từ một phía duy nhất — hoặc từ bên trái (ký hiệu là ![]() ) hoặc từ bên phải (ký hiệu là
) hoặc từ bên phải (ký hiệu là ![]() ).
).
Dưới đây là một số ví dụ cụ thể về giới hạn một bên:
📌 Ví dụ 1:
Tính giới hạn sau:
![]()
🔎 Giải:
- Khi
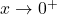 , tức là
, tức là 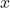 tiến đến 0 từ phía dương (số dương rất nhỏ).
tiến đến 0 từ phía dương (số dương rất nhỏ). - Khi đó $\frac{1}{x} \to +\infty$
✅ Kết luận:
![]()
📌 Ví dụ 2:
Tính giới hạn:
![]()
🔎 Giải:
- Khi $x \to 0^-$, tức là $x$ tiến đến 0 từ phía âm (số âm rất nhỏ).
- Khi đó $\frac{1}{x} \to -\infty$
✅ Kết luận:
![]()
📌 Ví dụ 3:
Xét hàm số bậc thang:
![Rendered by QuickLaTeX.com \[f(x) = \begin{cases}1 & \text{khi } x < 2 \\3 & \text{khi } x \geq 2\end{cases}\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-9d975da11fc42961526c8e0a8325cb05_l3.png)
Tính các giới hạn:
🔎 Giải:
✅ Kết luận:
- Giới hạn trái khác giới hạn phải, nên giới hạn
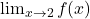 không tồn tại.
không tồn tại.