







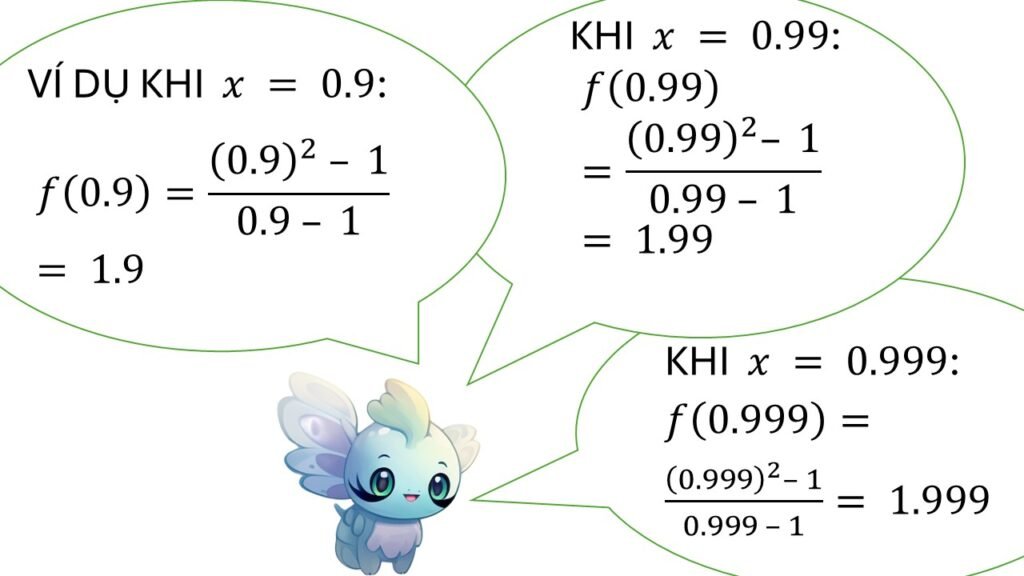
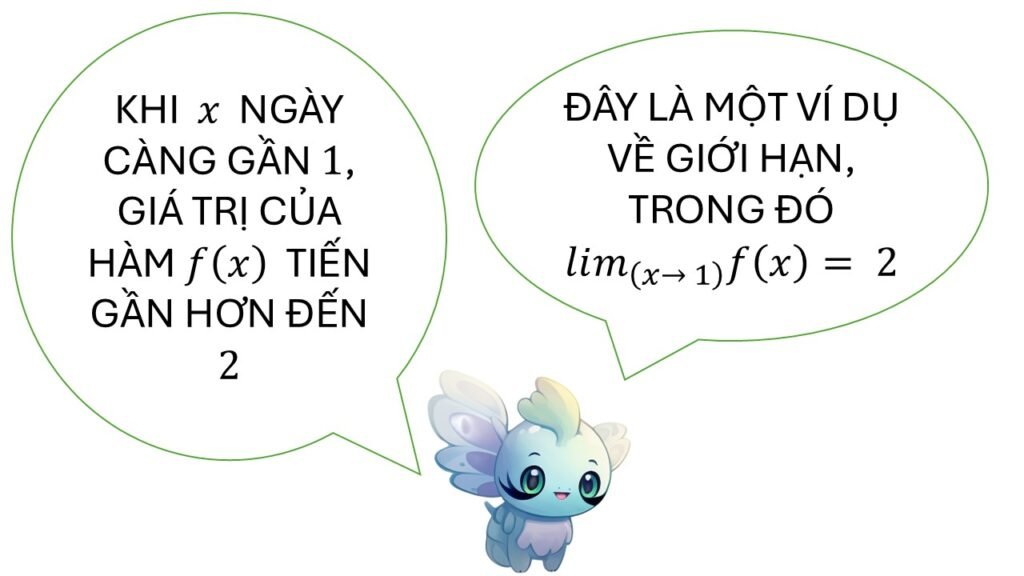
Giới hạn như… bạn nhìn crush từ xa
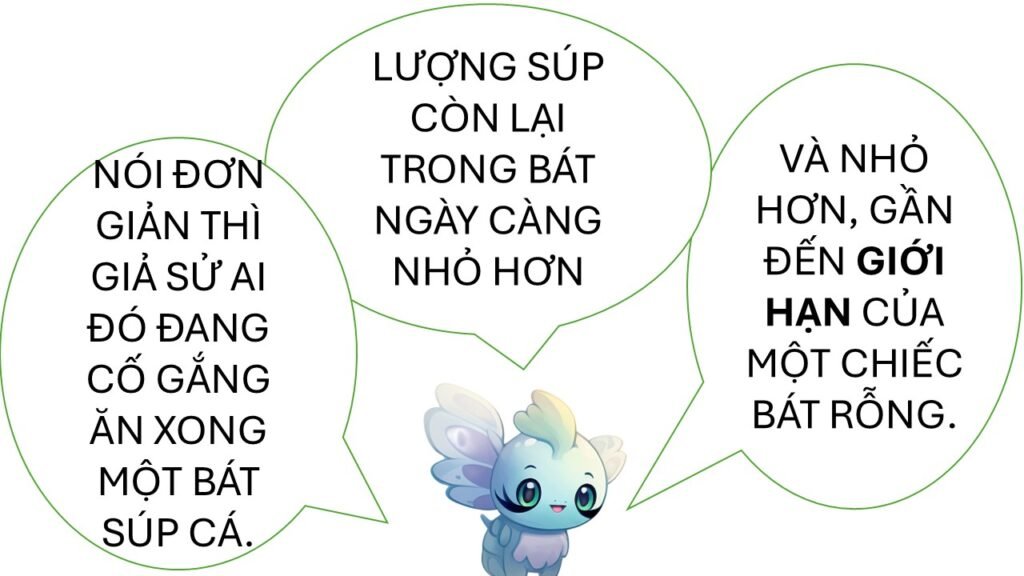
Bạn đang đứng ở hành lang, thấy crush đang đi về phía bạn. Tim đập thình thịch, bạn hồi hộp theo dõi… nhưng crush rẽ vào lớp trước khi kịp tới gần! Bạn biết là người ta gần như đến, nhưng trái tim cô ấy chưa bao giờ thật sự đến chỗ bạn.
Chính là như vậy đó! Giới hạn là giá trị hàm số tiến tới khi biến tiến đến một điểm nào đó — nhưng không nhất thiết phải đến!
Ký hiệu giới hạn của hàm số ![]() khi
khi ![]() tiến đến
tiến đến ![]() là
là ![]() được viết là:
được viết là:![]()
và nó là giá trị mà hàm số tiến dần đến khi biến số của nó tiến dần đến một giá trị nhất định. Ta đọc là: “Giới hạn của hàm số f(x) khi x tiến tới a là L”.
📘 Định nghĩa chi tiết: Giới hạn tại điểm ![]()
Cho hàm số ![]() , ta nói:
, ta nói:
![]()
nếu với mọi số thực dương ![]() , luôn tồn tại một số
, luôn tồn tại một số ![]() sao cho:
sao cho:
![]()
Nghĩa là: chỉ cần ta chọn ![]() đủ gần
đủ gần ![]() , thì
, thì ![]() sẽ đủ gần
sẽ đủ gần ![]() .
.
Như vậy, giới hạn mô tả hành vi của hàm số tại một điểm lân cận, chứ không nhất thiết là giá trị của hàm số tại chính điểm đó.
![]() : khoảng sai số ta chấp nhận giữa
: khoảng sai số ta chấp nhận giữa ![]() và giá trị giới hạn
và giá trị giới hạn ![]() .
.
![]() : khoảng cách ta cần
: khoảng cách ta cần ![]() nằm trong đó (gần
nằm trong đó (gần ![]() ) để đảm bảo
) để đảm bảo ![]() nằm gần
nằm gần ![]() .
.
💘 Mô hình hóa: Khoảng cách giữa 2 trái tim
Giả sử:
- Trái tim của bạn đứng yên tại vị trí
 .
. - Trái tim của crush chuyển động về phía bạn theo hàm:
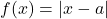
→ Đây là khoảng cách giữa 2 trái tim tại thời điểm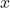 , khi crush tiến đến gần bạn.
, khi crush tiến đến gần bạn.
📉 Giới hạn khi crush tiến lại gần
Khi crush càng tiến sát tới bạn từ hành lang, tức là ![]() , thì khoảng cách giữa hai trái tim sẽ tiến đến:
, thì khoảng cách giữa hai trái tim sẽ tiến đến:
![]()
💡 Có nghĩa là: khoảng cách gần bằng 0 nhưng không bao giờ bằng 0, bởi crush rẽ vào lớp ngay trước khi tới sát tim bạn, và không thèm nhìn bạn 🤭
✨ Biểu diễn định nghĩa ε–δ cho tình huống “2 trái tim không gặp nhau”
Dù hai trái tim không bao giờ chạm nhau, ta vẫn có thể nói rằng:![]()
vì theo định nghĩa:
với mọi số thực dương ![]() , luôn tồn tại một số
, luôn tồn tại một số ![]() sao cho:
sao cho:
![]()
→ Miễn là crush tiến đủ gần, khoảng cách có thể nhỏ đến mức trái tim bạn “vỡ òa” — dù thực tế là chưa chạm đến! 🥲
Ví dụ
Xét một cái máy “Đo Độ Hào Hứng”, ký hiệu là \)f(x)\).
Nguyên tắc của máy: Độ hào hứng ![]() sẽ bằng số người rủ bạn đi chơi (
sẽ bằng số người rủ bạn đi chơi (![]() ) cộng thêm 2.
) cộng thêm 2.![]()
Bây giờ ta muốn tìm giới hạn độ hào hứng khi số người rủ bạn đi chơi tiến gần đến 3.![]()
Cùng làm “thám tử” nào:
- Khi có 2.9 người rủ (chắc 1 người đang lưỡng lự): Độ hào hứng là
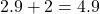 .
. - Khi có 2.999 người rủ (người đó sắp quyết định rồi): Độ hào hứng là
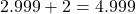 .
. - Khi có 3.001 người rủ (vừa có thêm 1 người hóng hớt muốn đi cùng): Độ hào hứng là
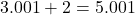 .
.
Thấy gì không? Khi số người rủ rê (![]() ) tiến sát nút đến 3, thì độ hào hứng của bạn (
) tiến sát nút đến 3, thì độ hào hứng của bạn (![]() ) cũng đang nhắm thẳng đến con số 5.
) cũng đang nhắm thẳng đến con số 5.
Vậy ta kết luận:![]()
Đó, giới hạn chỉ đơn giản là cái đích mà hàm số đang “lao tới” thôi! 😉
Ví dụ 2
Xét biểu diễn toán học hơn của ví dụ trước:
Xét hàm số ![]() . Ta hãy xem xét giới hạn của hàm số này khi
. Ta hãy xem xét giới hạn của hàm số này khi ![]() tiến đến 3.
tiến đến 3.
![]()
Để tìm giới hạn này, chúng ta có thể xem xét các giá trị của ![]() khi
khi ![]() nhận các giá trị ngày càng gần với 3 từ cả hai phía (nhỏ hơn 3 và lớn hơn 3).
nhận các giá trị ngày càng gần với 3 từ cả hai phía (nhỏ hơn 3 và lớn hơn 3).
| x | f(x) = x + 2 |
| 2.9 | 4.9 |
| 2.99 | 4.99 |
| 2.999 | 4.999 |
| 3 | ? |
| 3.001 | 5.001 |
| 3.01 | 5.01 |
| 3.1 | 5.1 |
Từ bảng trên, ta có thể thấy rằng khi ![]() càng tiến gần đến 3, giá trị của
càng tiến gần đến 3, giá trị của ![]() càng tiến gần đến 5. Do đó, ta có thể kết luận rằng:
càng tiến gần đến 5. Do đó, ta có thể kết luận rằng:
![]()
Trong trường hợp này, giá trị của hàm số tại ![]() cũng là 5 (tức là
cũng là 5 (tức là ![]() ). Tuy nhiên, điều quan trọng cần nhớ là giới hạn không quan tâm đến giá trị thực sự của hàm số tại điểm đó, mà chỉ quan tâm đến giá trị mà nó đang tiến đến.
). Tuy nhiên, điều quan trọng cần nhớ là giới hạn không quan tâm đến giá trị thực sự của hàm số tại điểm đó, mà chỉ quan tâm đến giá trị mà nó đang tiến đến.
📐 Ví dụ minh hoạ 3
Xét hàm:![]()
Ta tính:![]()
Với bất kỳ ![]() , ta cần:
, ta cần:![]()
→ Chọn ![]() là thỏa điều kiện!
là thỏa điều kiện!
