📘 “Tiệm cận” là một khái niệm trong toán học dùng để diễn tả khi một đại lượng tiến gần đến một giá trị nào đó, mà không bao giờ chạm tới – giống như bạn đi mãi về phía chân trời, nhưng không bao giờ thực sự tới nơi.
🧮 Giải thích bằng dãy số
Giả sử bạn có một dãy số:
![]()
- Khi
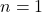 ,
, 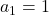
- Khi
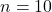 ,
, 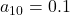
- Khi
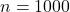 ,
, 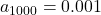
👉 Giá trị của ![]() ngày càng nhỏ, tiến tới 0, nhưng không bao giờ bằng 0
ngày càng nhỏ, tiến tới 0, nhưng không bao giờ bằng 0
Ta nói rằng giới hạn của dãy ![]() là 0, tức là:
là 0, tức là:
![]()
⏳ 0 chính là giá trị tiệm cận của dãy.
Niêu cơm không bao giờ cạn
sau đó, chúng ta sẽ chứng minh rằng mỗi niêu cơm bình thường đều không bao giờ cạn như niêu cơm của Thạch Sanh dựa trên giới hạn dãy số
🔍 Phân tích toán học
Giả sử ta bắt đầu với 1 bát cơm đầy. Mỗi lần ăn, ta lấy một nửa phần còn lại:
- Lần 1: ăn
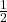
- Lần 2: ăn
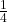
- Lần 3: ăn
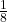
- …
- Lần
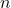 : ăn
: ăn 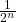
Tổng lượng cơm đã ăn sau ![]() lần là:
lần là:
![]()
Đây là một dãy cấp số nhân với công bội
👉 Khi ![]() :
:
![]()
Nghĩa là, tổng lượng cơm ăn được tiến tới 1, nhưng không bao giờ chạm tới 1.
🧠 Kết luận
Niêu cơm không bao giờ cạn vì lượng cơm ăn mỗi lần ngày càng nhỏ, tiến tới 0.
- Tuy ta ăn gần hết, nhưng luôn còn một chút – nhỏ đến mức tưởng như không còn gì.