ước lượng hợp lý cực đại (Maximum Likelihood Estimation - MLE) cho phân phối Bernoulli

Phân phối Bernoulli mô tả một thử nghiệm với hai kết quả: “thành công” (1) hoặc “thất bại” (0), với xác suất thành công là $p$ . Ví dụ, bạn ném một đồng xu và muốn biết xác suất $p$ để đồng xu ra mặt ngửa (1). Dữ liệu là các lần ném: $X = {x_1, x_2, \dots, x_n}$ , trong đó $x_i = 1$ (ngửa) hoặc $x_i = 0$ (sấp).

Giả sử bạn là một nhà ảo thuật, muốn đoán xác suất một khán giả chọn lá bài “Át Bích” (thành công) khi rút ngẫu nhiên từ bộ bài. Bạn quan sát 100 lần rút bài và ghi lại kết quả.

Bước 1: Hàm hợp lý (Likelihood Function)

Phân phối Bernoulli có hàm khối xác suất:
$f(x_i | p) = p^{x_i} (1 - p)^{1 - x_i}, \quad x_i \in {0, 1}$
Giả sử các quan sát $x_i$ độc lập và cùng phân phối (i.i.d.), hàm hợp lý cho dữ liệu $X = {x_1, x_2, \dots, x_n}$ là:
$L(p | X) = \prod_{i=1}^n p^{x_i} (1 - p)^{1 - x_i} = p^{\sum_{i=1}^n x_i} (1 - p)^{n - \sum_{i=1}^n x_i}$
Trong đó, $\sum_{i=1}^n x_i$ là số lần “thành công” (ví dụ: số lần rút được Át Bích).

Log-hàm hợp lý:
$\ell(p | X) = \log L(p | X) = \log \left( p^{\sum_{i=1}^n x_i} (1 - p)^{n - \sum_{i=1}^n x_i} \right)$
$= \left( \sum_{i=1}^n x_i \right) \log p + \left( n - \sum_{i=1}^n x_i \right) \log (1 - p)$

Bước 2: Tìm ước lượng MLE

Để tìm $\hat{p}$ , ta tối ưu hóa $\ell(p | X)$ bằng cách lấy đạo hàm và đặt bằng 0:
$\frac{\partial \ell}{\partial p} = \frac{\sum_{i=1}^n x_i}{p} - \frac{n - \sum_{i=1}^n x_i}{1 - p} = 0$
Giải phương trình:
$\frac{\sum_{i=1}^n x_i}{p} = \frac{n - \sum_{i=1}^n x_i}{1 - p}$
Nhân chéo:
$\left( \sum_{i=1}^n x_i \right) (1 - p) = \left( n - \sum_{i=1}^n x_i \right) p$
$\sum_{i=1}^n x_i - p \sum_{i=1}^n x_i = n p - p \sum_{i=1}^n x_i$
$\sum_{i=1}^n x_i = n p$
$\hat{p} = \frac{\sum_{i=1}^n x_i}{n}$
Kết quả: $\hat{p}$ là tỷ lệ thành công trong mẫu, tức là trung bình của các $x_i$ . Ví dụ, nếu bạn rút được Át Bích 25 lần trong 100 lần, thì $\hat{p} = \frac{25}{100} = 0.25$ .

Bước 3: Kiểm tra cực trị bằng đạo hàm bậc hai

Để xác nhận $\hat{p}$ là cực đại, ta tính đạo hàm bậc hai của $\ell(p | X)$ và kiểm tra tại $\hat{p}$ .

Đạo hàm bậc nhất (tính lại cho rõ):
$\frac{\partial \ell}{\partial p} = \frac{\sum_{i=1}^n x_i}{p} - \frac{n - \sum_{i=1}^n x_i}{1 - p}$

Đạo hàm bậc hai:
$\frac{\partial^2 \ell}{\partial p^2} = \frac{\partial}{\partial p} \left( \frac{\sum_{i=1}^n x_i}{p} - \frac{n - \sum_{i=1}^n x_i}{1 - p} \right)$

Phần thứ nhất: $\frac{\partial}{\partial p} \left( \frac{\sum_{i=1}^n x_i}{p} \right) = -\frac{\sum_{i=1}^n x_i}{p^2}$
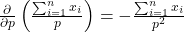
Phần thứ hai: $\frac{\partial}{\partial p} \left( -\frac{n - \sum_{i=1}^n x_i}{1 - p} \right) = -\frac{-(n - \sum_{i=1}^n x_i)}{(1 - p)^2} = -\frac{n - \sum_{i=1}^n x_i}{(1 - p)^2}$

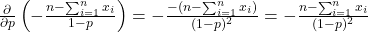
Kết hợp:
$\frac{\partial^2 \ell}{\partial p^2} = -\frac{\sum_{i=1}^n x_i}{p^2} - \frac{n - \sum_{i=1}^n x_i}{(1 - p)^2}$
Thay $\hat{p} = \frac{\sum_{i=1}^n x_i}{n}$ , và đặt $s = \sum_{i=1}^n x_i$ , ta có:

$p = \hat{p} = \frac{s}{n}$
$1 - \hat{p} = 1 - \frac{s}{n} = \frac{n - s}{n}$

Thay vào đạo hàm bậc hai:
$\frac{\partial^2 \ell}{\partial p^2} \bigg|{\hat{p}} = -\frac{s}{\left(\frac{s}{n}\right)^2} - \frac{n - s}{\left(\frac{n - s}{n}\right)^2}$ $= -\frac{s}{\frac{s^2}{n^2}} - \frac{n - s}{\frac{(n - s)^2}{n^2}} = -\frac{n^2 s}{s^2} - \frac{n^2 (n - s)}{(n - s)^2} = -\frac{n^2}{s} - \frac{n^2}{n - s}$ $= -n^2 \left( \frac{1}{s} + \frac{1}{n - s} \right) = -n^2 \cdot \frac{n - s + s}{s (n - s)} = -\frac{n^3}{s (n - s)}$ Vì $n > 0$ , $s = \sum{i=1}^n x_i \geq 0$ , và $n - s \geq 0$ , nên $\frac{n^3}{s (n - s)} \geq 0$ . Do đó:
$\frac{\partial^2 \ell}{\partial p^2} \bigg|_{\hat{p}} \leq 0$

Kết luận

MLE cho phân phối Bernoulli cho ra $\hat{p} = \frac{\sum_{i=1}^n x_i}{n}$ , là tỷ lệ thành công trong mẫu.

Ví dụ minh họa

Giả sử bạn quan sát 10 lần rút bài, với kết quả: $X = {1, 0, 1, 0, 0, 1, 0, 1, 0, 1}$ (1 là rút được Át Bích, 0 là không).

Số lần thành công: $s = \sum_{i=1}^n x_i = 5$ .
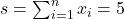Số lần thử: $n = 10$ .
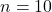Ước lượng MLE: $\hat{p} = \frac{5}{10} = 0.5$ .

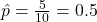Đạo hàm bậc hai tại $\hat{p} = 0.5$ :
$\frac{\partial^2 \ell}{\partial p^2} \bigg|_{\hat{p}=0.5} = -\frac{10^3}{5 \cdot (10 - 5)} = -\frac{1000}{25} = -40 < 0$
Xác nhận $\hat{p} = 0.5$ là cực đại.

ước lượng hợp lý cực đại (Maximum Likelihood Estimation – MLE) cho phân phối Bernoulli

Bước 1: Hàm hợp lý (Likelihood Function)

Bước 2: Tìm ước lượng MLE

Bước 3: Kiểm tra cực trị bằng đạo hàm bậc hai

Kết luận

Ví dụ minh họa

Để lại một bình luận Hủy

Bước 1: Hàm hợp lý (Likelihood Function)

Bước 2: Tìm ước lượng MLE

Bước 3: Kiểm tra cực trị bằng đạo hàm bậc hai

Kết luận

Ví dụ minh họa

Related Posts

Để lại một bình luận Hủy