Phân phối Poisson mô tả số lần xảy ra của một sự kiện ngẫu nhiên trong một khoảng thời gian hoặc không gian cố định, với tham số ![]() , biểu thị số lần xảy ra trung bình (rate). Ví dụ,
, biểu thị số lần xảy ra trung bình (rate). Ví dụ, ![]() là số trung bình khách đến một quán phở trong 1 giờ.
là số trung bình khách đến một quán phở trong 1 giờ.
Tình huống vui: Bạn là chủ quán phở, muốn đoán số khách trung bình mỗi giờ (![]() ) dựa trên số lượng khách đến trong 10 giờ quan sát:
) dựa trên số lượng khách đến trong 10 giờ quan sát: ![]() , với
, với ![]() là số khách đến trong giờ thứ
là số khách đến trong giờ thứ ![]() .
.
Bước 1: Hàm hợp lý (Likelihood Function)
Phân phối Poisson có hàm khối xác suất:![]()
Giả sử các quan sát ![]() độc lập và cùng phân phối (i.i.d.), hàm hợp lý cho dữ liệu
độc lập và cùng phân phối (i.i.d.), hàm hợp lý cho dữ liệu ![]() là:
là:![]()
Vì ![]() không phụ thuộc vào
không phụ thuộc vào ![]() , ta có thể bỏ qua khi tối ưu. Log-hàm hợp lý:
, ta có thể bỏ qua khi tối ưu. Log-hàm hợp lý:![]()
![]()
Bỏ hằng số ![]() :
:![]()
Bước 2: Tìm ước lượng MLE
Tối ưu ![]() bằng cách lấy đạo hàm và đặt bằng 0:
bằng cách lấy đạo hàm và đặt bằng 0:![]()
Giải:![]()
Kết quả: ![]() là trung bình mẫu của số khách mỗi giờ. Ví dụ, nếu bạn ghi nhận số khách trong 10 giờ là
là trung bình mẫu của số khách mỗi giờ. Ví dụ, nếu bạn ghi nhận số khách trong 10 giờ là ![]() , thì:
, thì:![]()
Bước 3: Kiểm tra cực trị bằng đạo hàm bậc hai
Để xác nhận ![]() là cực đại, ta tính đạo hàm bậc hai:
là cực đại, ta tính đạo hàm bậc hai:![]()
Tính đạo hàm bậc hai:![]()
Tại ![]() :
: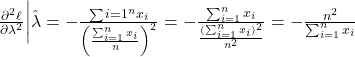
Vì ![]() và
và ![]() , nên:
, nên:
Nếu ![]() (có ít nhất một khách), thì
(có ít nhất một khách), thì ![]() , xác nhận
, xác nhận ![]() là cực đại cục bộ.
là cực đại cục bộ.
Kết luận
MLE cho phân phối Poisson cho ra ![]() , là trung bình mẫu. Đạo hàm bậc hai xác nhận đây là điểm cực đại khi
, là trung bình mẫu. Đạo hàm bậc hai xác nhận đây là điểm cực đại khi ![]() .
.
Ví dụ minh họa
Quay lại quán phở, bạn quan sát số khách trong 10 giờ: ![]() .
.
- Tổng:
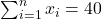 ,
, 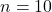 .
. - Ước lượng MLE:
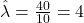 (trung bình 4 khách/giờ).
(trung bình 4 khách/giờ). - Đạo hàm bậc hai tại
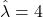 :
: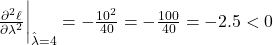
Xác nhận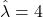 là cực đại.
là cực đại.