K-Nearest Neighbors (KNN): có vấn đề gì thì hỏi hàng xóm

KNN là một thuật toán cực kỳ đơn giản nhưng rất thông minh trong thế giới máy học. Nó giống như bạn đang hỏi ý kiến của những người hàng xóm thân thiện để đưa ra quyết định.

Câu chuyện vui: KNN trong đời thực

Giả sử bạn mới chuyển đến một khu phố và muốn biết nhà hàng pizza nào ngon nhất. Nhưng bạn chưa biết chọn quán nào.

Bạn đi hỏi 3 người hàng xóm gần nhất (đây chính là “K=3” trong KNN đó). Mỗi người nói họ thích quán A, quán B, quán A. Vì số đông thích quán A, bạn quyết định chọn quán A để thưởng thức.

KNN cũng y hệt vậy: khi muốn phân loại một điểm dữ liệu mới, KNN sẽ nhìn vào “K” điểm dữ liệu gần nó nhất, xem đa số thuộc nhóm nào, rồi “bê” nhóm đó cho điểm mới.

Cách hoạt động của KNN

Bạn có một “bản đồ” (dữ liệu) với nhiều điểm đã biết nhóm (label) của chúng.
Bạn muốn biết điểm mới này thuộc nhóm nào.
Bạn đo khoảng cách từ điểm mới đến tất cả các điểm đã biết trên bản đồ.
Chọn ra K điểm gần nhất.
Xem nhóm nào chiếm đa số trong K điểm đó, điểm mới sẽ thuộc nhóm đó.

Ví dụ dễ hiểu

K = 5 (hỏi 5 người hàng xóm)
5 người đó có 3 người thích nhóm “Táo” (Apple), 2 người thích nhóm “Cam” (Orange)
Điểm mới sẽ được xếp vào nhóm “Táo”.

Một số điểm vui:

Nếu bạn hỏi ít người quá (K=1), bạn dễ bị “bịp” bởi một người hàng xóm quá lắm khen hoặc chê thôi.
Nếu bạn hỏi quá nhiều người (K rất lớn), bạn có thể nhận được ý kiến quá lộn xộn, khó quyết định.
KNN không “học” theo kiểu phức tạp, nó chỉ đơn giản là “hỏi ý kiến hàng xóm gần nhất”.

Tóm tắt

KNN là thuật toán “hỏi thăm hàng xóm” để quyết định điểm mới thuộc nhóm nào.

Bạn như người mới, “hỏi nhanh 3, 5, hay 7 ông bà hàng xóm, nghe họ bảo gì thì nghe theo.” Đơn giản mà hiệu quả! Đó gọi là “ba ông thợ da bằng một Gia Cát Lượng”

chi tiết hơn

Quy trình phân loại và hồi quy

Khi một điểm dữ liệu mới (điểm truy vấn) cần được phân loại hoặc dự đoán giá trị, thuật toán KNN tuân theo một chuỗi ba bước cơ bản và tuần tự:

Tính toán khoảng cách: Bước đầu tiên và quan trọng nhất là tính toán khoảng cách từ điểm dữ liệu mới đến tất cả các điểm dữ liệu hiện có trong tập huấn luyện. Các độ đo khoảng cách khác nhau có thể được sử dụng tùy thuộc vào bản chất của dữ liệu và bài toán, với khoảng cách Euclidean là một lựa chọn phổ biến.
Chọn K láng giềng gần nhất: Sau khi tính toán tất cả các khoảng cách, thuật toán sẽ sắp xếp các điểm dữ liệu trong tập huấn luyện theo thứ tự tăng dần của khoảng cách đến điểm truy vấn. Từ danh sách đã sắp xếp này, nó chọn ra ‘K’ điểm dữ liệu có khoảng cách nhỏ nhất, tức là K láng giềng gần nhất.
Dự đoán:

Đối với phân loại: Điểm dữ liệu mới được gán cho lớp (class label) xuất hiện thường xuyên nhất (majority vote) trong số K láng giềng gần nhất đã chọn. Điều này được gọi là “bỏ phiếu đa số”.
Đối với hồi quy: Giá trị dự đoán cho điểm dữ liệu mới là giá trị trung bình (mean) của các giá trị mục tiêu (target values) của K láng giềng gần nhất.

Ví dụ minh họa rõ ràng ảnh hưởng của việc lựa chọn K: giả sử có một điểm dữ liệu mới cần phân loại và hai lớp A và B. Nếu K=3, và trong 3 láng giềng gần nhất, có 2 điểm thuộc lớp B và 1 điểm thuộc lớp A, thì điểm mới sẽ được phân loại là lớp B. Ngược lại, nếu K=7, và trong 7 láng giềng gần nhất, có 5 điểm thuộc lớp A và 2 điểm thuộc lớp B, thì điểm mới sẽ được phân loại là lớp A.

Các độ đo khoảng cách phổ biến

Việc lựa chọn độ đo khoảng cách (distance metric) phù hợp là một quyết định quan trọng trong KNN, vì nó trực tiếp định lượng sự tương đồng hoặc “gần gũi” giữa các điểm dữ liệu trong không gian đặc trưng. Sự lựa chọn này có ảnh hưởng trực tiếp đến cách thuật toán xác định các láng giềng và từ đó tác động đến độ chính xác và hiệu suất tổng thể của mô hình.

Các độ đo khoảng cách phổ biến được sử dụng trong KNN bao gồm:

Euclidean Distance (Khoảng cách Euclidean): Đây là độ đo khoảng cách được sử dụng phổ biến nhất và thường là mặc định trong nhiều thư viện học máy, bao gồm Scikit-learn của Python. Nó đo khoảng cách đường thẳng (straight-line distance) giữa hai điểm trong không gian đa chiều. Công thức của khoảng cách Euclidean giữa hai điểm p và q trong không gian n chiều là: 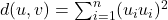$d(u,v)=\sum_{i=1}^n(u_i−u_i)^2$ . Độ đo này thích hợp cho dữ liệu số liên tục và khi các đặc trưng được chuẩn hóa tốt.
Manhattan Distance (Khoảng cách Manhattan / L1 Norm): Còn được gọi là khoảng cách “taxicab” hoặc “city block”. Nó đo khoảng cách di chuyển dọc theo các trục (ngang và dọc) trong một lưới, giống như cách một chiếc taxi di chuyển trong một thành phố. Công thức của khoảng cách Manhattan là tổng các giá trị tuyệt đối của sự khác biệt giữa các tọa độ tương ứng của hai điểm: 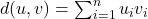$d(u,v)=\sum_{i=1}^n∣u_i−v_i∣$ . Độ đo này thường được sử dụng khi các đặc trưng đại diện cho các chuyển động trên một lưới hoặc khi dữ liệu ít nhạy cảm với ngoại lệ.
Minkowski Distance: Đây là một dạng tổng quát của khoảng cách Euclidean và Manhattan. Nó được định nghĩa bởi một tham số ‘p’. Khi p=1, khoảng cách Minkowski trở thành khoảng cách Manhattan; khi p=2, nó trở thành khoảng cách Euclidean. Điều này cho phép điều chỉnh độ đo sự tương đồng tùy thuộc vào bản chất của dữ liệu.
Chebyshev Distance: Đo khoảng cách tối đa giữa hai điểm dọc theo bất kỳ chiều nào. Nó thích hợp khi các đặc trưng đại diện cho các chuyển động theo lưới với tầm quan trọng ngang nhau, ví dụ như trong các trò chơi cờ.
Cosine Similarity (Độ tương đồng Cosine): Đo lường sự tương đồng giữa hai vector dựa trên cosine của góc giữa chúng. Giá trị của nó nằm trong khoảng từ 0 (rất giống) đến 1 (hoàn toàn khác), mặc dù trong một số định nghĩa, nó có thể nằm trong khoảng [-1, 1] cho các vector có hướng. Độ đo này đặc biệt hữu ích trong phân tích văn bản để so sánh sự tương đồng giữa các tài liệu dựa trên tần suất từ, hoặc trong các không gian chiều cao nơi hướng của vector quan trọng hơn độ lớn của nó.

Việc lựa chọn độ đo khoảng cách không phải là một quyết định tùy tiện mà là một siêu tham số quan trọng định hình cách KNN hiểu “sự tương đồng” và do đó ảnh hưởng trực tiếp đến ranh giới quyết định của nó. Sự lựa chọn này phải được dẫn dắt bởi bản chất của dữ liệu và bài toán cụ thể, chứ không chỉ dựa vào sự tiện lợi của độ đo mặc định. Ví dụ, khoảng cách Euclidean giả định các đặc trưng có tầm quan trọng tương đương và không bị ảnh hưởng bởi hướng, trong khi khoảng cách Manhattan mạnh mẽ hơn với các ngoại lệ và phù hợp với dữ liệu có cấu trúc dạng lưới. Điều này cho thấy rằng việc hiểu rõ các thuộc tính toán học của từng độ đo khoảng cách là cần thiết để chọn ra phương pháp tối ưu, đảm bảo rằng “sự gần gũi” được xác định một cách có ý nghĩa và đóng góp vào độ chính xác của mô hình.