Giả sử dữ liệu ![]() từ phân phối chuẩn
từ phân phối chuẩn ![]() , và bạn muốn ước lượng
, và bạn muốn ước lượng ![]() .
.
Hàm mật độ:![]()
Log-hàm hợp lý:![]()
Tối ưu hóa:
- Đối với
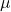 :
: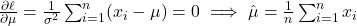
(Trung bình mẫu). - Đối với
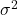 :
: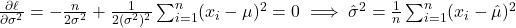
(Phương sai mẫu).
Kết quả: ![]() và
và ![]() là các ước lượng hợp lý cực đại, giống như tìm ra công thức phở với 2.5 thìa muối và 5 lát thịt bò!
là các ước lượng hợp lý cực đại, giống như tìm ra công thức phở với 2.5 thìa muối và 5 lát thịt bò!
Bây giờ, ta tính đạo hàm bậc hai theo ![]() và
và ![]() , sau đó đánh giá tại
, sau đó đánh giá tại ![]() để xác định tính chất cực trị.
để xác định tính chất cực trị.
Đạo hàm bậc hai theo ![]()
Lấy đạo hàm của ![]() theo
theo ![]() :
:![]()
Đạo hàm bậc hai này không phụ thuộc vào ![]() , nên tại
, nên tại ![]() :
:![]()
Vì ![]() và
và ![]() , nên
, nên ![]() , tức là log-hàm hợp lý đạt cực đại theo
, tức là log-hàm hợp lý đạt cực đại theo ![]() tại
tại ![]() .
.
Đạo hàm bậc hai theo ![]()
Lấy đạo hàm của ![]() theo
theo ![]() :
:![]()
Tính đạo hàm:
- Phần thứ nhất:
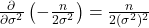
- Phần thứ hai:
![Rendered by QuickLaTeX.com \frac{\partial}{\partial \sigma^2} \left[ \frac{1}{2(\sigma^2)^2} \sum_{i=1}^n (x_i - \mu)^2 \right] = -\frac{1}{(\sigma^2)^3} \sum_{i=1}^n (x_i - \mu)^2](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-de472d5b48a1fdeb63fc701374fb3de3_l3.png)
Kết hợp: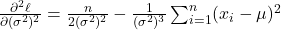
Tại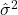 và
và 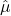 :
: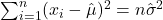
Thay vào: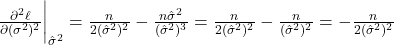
Vì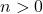 và
và  , nên
, nên 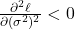 , tức là log-hàm hợp lý đạt cực đại theo
, tức là log-hàm hợp lý đạt cực đại theo 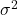 tại
tại 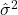 .
.
Discover more from Cùng Học Cùng Mơ
Subscribe to get the latest posts sent to your email.