Phân Phối Đều và Ứng Dụng Thực Tế

Phân phối đều (Uniform distribution) là một loại phân phối xác suất trong đó tất cả các giá trị trong một khoảng đều có xác suất xuất hiện bằng nhau. Có hai loại phân phối đều chính:

1. Phân phối đều rời rạc (Discrete Uniform Distribution):

Đây là phân phối mà các giá trị rời rạc có xác suất xuất hiện như nhau. Ví dụ điển hình là khi tung một con xúc xắc chuẩn, mỗi mặt (1, 2, 3, 4, 5, 6) có xác suất xuất hiện bằng nhau.

Nếu có n giá trị có thể xảy ra, xác suất của mỗi giá trị sẽ là:

2. Phân phối đều liên tục (Continuous Uniform Distribution):

Trong phân phối đều liên tục, các giá trị trong một khoảng liên tục đều có xác suất bằng nhau. Ví dụ, nếu bạn chọn ngẫu nhiên một số trong khoảng từ a đến b, mọi số trong khoảng đó có khả năng xuất hiện như nhau.

Hàm mật độ xác suất (PDF) của phân phối đều liên tục trên khoảng là:

Tính chất của phân phối đều:

• Trung bình của phân phối đều liên tục là:
  
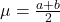
• Phương sai là:
  

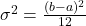
Ví dụ:

1. Phân phối đều rời rạc: Khi tung một đồng xu, xác suất xuất hiện mặt sấp hoặc mặt ngửa đều bằng .
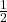2. Phân phối đều liên tục: Giả sử nhiệt độ mỗi ngày trong một mùa nào đó dao động từ 20°C đến 30°C và mỗi giá trị trong khoảng này có khả năng xuất hiện như nhau, thì đây là một ví dụ của phân phối đều liên tục trên khoảng .

Phân phối đều được sử dụng trong các bài toán liên quan đến ngẫu nhiên và xác suất mà mỗi kết quả có thể xảy ra với xác suất như nhau.

Khái Niệm Phân Phối Đều

Phân phối đều, thường được gọi trong tiếng Anh là “uniform distribution,” là một trong những khái niệm cơ bản trong toán học và thống kê. Nó mô tả một loại phân phối mà trong đó mọi giá trị trong một khoảng nhất định có khả năng xuất hiện với xác suất giống nhau. Nghĩa là, nếu một biến ngẫu nhiên được phân phối đều trong một khoảng từ a đến b, thì xác suất để nó nhận giá trị bất kỳ trong khoảng này là như nhau. Đặc điểm nổi bật của loại hình phân phối này là sự đồng đều trong khả năng xảy ra của các giá trị.

Các ví dụ cụ thể về phân phối đều có thể được tìm thấy trong nhiều lĩnh vực. Trong toán học, khi một đồng xu được tung lên, xác suất để nó rơi vào mặt sấp hoặc mặt ngửa là như nhau, tức là mỗi mặt có xác suất 50%. Tương tự, trong thống kê, khi một số được chọn ngẫu nhiên từ khoảng [1, 10], tất cả các số nguyên đều có khả năng xuất hiện bằng nhau, đó là một ví dụ tiêu biểu về phân phối đều. Trong lĩnh vực kỹ thuật, nhiều ứng dụng mở rộng sử dụng giả định phân phối đều để thiết kế các hệ thống, chẳng hạn như trong mô hình hóa dữ liệu và phân tích độ tin cậy.

Phân phối đều không chỉ giới hạn ở lý thuyết mà còn có vai trò quan trọng trong thực tiễn. Việc hiểu và áp dụng phân phối đều có thể giúp các nhà phân tích và kỹ sư trong việc thiết kế các hệ thống hiệu quả hơn. Nó cung cấp một nền tảng cho việc thực hiện các phân tích xác suất và quyết định trong các lĩnh vực như nghiên cứu hành vi người tiêu dùng, bảo trì máy móc hoặc tối ưu hóa quy trình sản xuất.

Tính Chất và Đặc Điểm Của Phân Phối Đều

Phân phối đều, hay còn gọi là phân phối đồng nhất, là một khái niệm quan trọng trong thống kê mà nhiều lĩnh vực nghiên cứu đều áp dụng. Một trong những tính chất chính của phân phối đều là các giá trị trong một khoảng nhất định có khả năng xuất hiện với cùng một xác suất. Điều này mang lại một sự phân bố cân bằng mà không có xu hướng tích tụ giá trị nào gần trung bình hay xa khỏi trung bình.

Trung bình của phân phối đều có thể được xác định bằng cách tính trung bình của các giá trị trong khoảng. Nếu một biến ngẫu nhiên Y được phân phối đều trong khoảng [a, b], thì trung bình của Y sẽ là (a + b) / 2. Độ lệch chuẩn, một chỉ số quan trọng thể hiện mức độ phân tán của dữ liệu, cũng đóng vai trò thiết yếu. Đối với phân phối đều, độ lệch chuẩn (σ) có thể được xác định bằng công thức σ = (b – a) / √12. Thông qua những chỉ số này, người sử dụng có thể nắm bắt được đặc điểm của phân phối đều một cách chính xác.

Các đặc điểm khác của phân phối đều bao gồm sự không đồng nhất ở sự tập trung của dữ liệu. Do đặc tính đồng nhất, phân phối đều cho thấy rằng mọi giá trị trong khoảng đều có xác suất xuất hiện như nhau, điều này làm cho nó trở thành một mô hình lý tưởng trong những trường hợp không có thông tin cụ thể nào về phân phối. Việc ứng dụng những đặc điểm này trong thực tế góp phần giúp các nhà nghiên cứu và thống kê xây dựng mô hình dự đoán và ra quyết định chính xác hơn.

Ứng Dụng Thực Tế Của Phân Phối Đều

Phân phối đều là một khái niệm quan trọng trong nhiều lĩnh vực khác nhau, từ kinh tế cho đến khoa học xã hội và kỹ thuật. Nguyên lý này được áp dụng rộng rãi trong các mô hình phân tích để giúp các nhà nghiên cứu khảo sát và đánh giá hiện tượng xảy ra trong xã hội hoặc trong thị trường. Một trong những ứng dụng nổi bật của phân phối đều trong kinh tế chính là việc phân tích doanh thu và chi phí trong một đợt nghiên cứu thị trường. Khi doanh thu của các sản phẩm được phân phối đều, có thể dễ dàng so sánh hiệu suất giữa các mặt hàng khác nhau, từ đó đưa ra quyết định đầu tư hợp lý.

Trong khoa học xã hội, việc ứng dụng phân phối đều thường xuất hiện trong các mô hình khảo sát dân số và đánh giá sự phân bổ tài nguyên. Ví dụ, khi một chính phủ triển khai các chương trình an sinh xã hội, việc phân phối đều các khoản trợ cấp đến các nhóm dân cư khác nhau có thể giúp đánh giá hiệu quả của chiến lược này. Sự phân bố đều này đảm bảo mọi người dân có cơ hội nhận được hỗ trợ và chất lượng cuộc sống được nâng cao một cách đồng đều.

Trong lĩnh vực kỹ thuật, phân phối đều cũng được áp dụng khi thiết kế và sản xuất các sản phẩm tiêu dùng, nhằm đảm bảo chất lượng và độ tin cậy. Chẳng hạn, trong lĩnh vực sản xuất pin, việc phân phối đều điện áp giữa các cell pin là rất quan trọng để tối ưu hóa hiệu suất và tuổi thọ của sản phẩm. Nhờ vào việc áp dụng nguyên lý phân phối đều, các kỹ sư và nhà nghiên cứu có thể kiểm soát chính xác các đặc tính cần thiết, từ đó nâng cao chất lượng sản phẩm cuối cùng.

Mối Quan Hệ Giữa Phân Phối Đều và Các Dạng Phân Phối Khác

Phân phối đều, một trong những dạng phân phối cơ bản trong thống kê, có những đặc điểm cũng như mối quan hệ thú vị với các dạng phân phối khác như phân phối chuẩn, phân phối nhị thức và phân phối Poisson. Phân phối đều được định nghĩa là một phân phối mà mọi giá trị trong một khoảng xác định đều có xác suất như nhau. Ngược lại, các dạng phân phối khác lại mang những đặc điểm riêng biệt, ảnh hưởng đến việc phân tích dữ liệu.

Phân phối chuẩn, hay còn gọi là phân phối Gaussian, là một dạng phân phối quan trọng trong thống kê với hình dạng đặc trưng của đường cong chuông. Khác với phân phối đều, phân phối chuẩn quy định rằng các giá trị quanh trung tâm sẽ có xác suất cao hơn. Điều này có nghĩa là trong khi phân phối đều không thiên lệch về một giá trị nào cả, phân phối chuẩn lại thể hiện sự tập trung dữ liệu quanh giá trị trung bình.

Phân phối nhị thức thì khác, khi nó mô tả xác suất của số thành công trong một số thử nghiệm nhất định có hai kết quả khả thi (thành công hoặc thất bại). Điều này tạo nên sự khác biệt so với phân phối đều, vì nó không đồng nhất trong xác suất mà phụ thuộc vào số lần thử nghiệm và xác suất thành công của mỗi lần thử.

Cuối cùng, phân phối Poisson dùng để mô tả số lần một sự kiện xảy ra trong một khoảng thời gian hoặc không gian cố định, thường được sử dụng khi các sự kiện xảy ra độc lập với nhau. Mặc dù không giống như phân phối đều, phân phối Poisson rất hữu ích trong việc phân tích các sự kiện hiếm xuất hiện. Thông qua việc so sánh những dạng phân phối này, người nghiên cứu có thể hiểu rõ hơn về vai trò của phân phối đều và cách nó giao thoa với các phương pháp phân tích thống kê khác.