Phân phối Poisson

Phân phối Poisson là một phân phối xác suất rời rạc, thường được sử dụng để mô tả số lần xảy ra của một sự kiện trong một khoảng thời gian cố định hoặc trong một không gian cố định, khi các sự kiện này xảy ra độc lập với nhau và với một tỷ lệ trung bình không đổi.

Các đặc điểm chính của phân phối Poisson:

1. Tham số (λ – lambda): Đây là tỷ lệ trung bình của các sự kiện xảy ra trong một đơn vị thời gian hoặc không gian. λ còn được gọi là tham số Poisson và cũng là giá trị kỳ vọng (mean) của phân phối.

Hàm xác suất (PMF):

Hàm xác suất của phân phối Poisson được cho bởi:

trong đó:

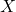• là số lần xảy ra của sự kiện.
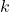• là số lần cụ thể mà bạn muốn tính xác suất.
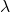• là tỷ lệ trung bình của các sự kiện xảy ra trong một đơn vị thời gian hoặc không gian.
• là cơ số của logarit tự nhiên (xấp xỉ 2.71828).

Kỳ vọng và phương sai:

• Kỳ vọng (mean):
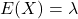
• Phương sai (variance):

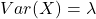
Ví dụ:

Giả sử một trung tâm dịch vụ khách hàng nhận trung bình 5 cuộc gọi mỗi giờ. Bạn muốn biết xác suất nhận được đúng 7 cuộc gọi trong một giờ. Trong trường hợp này:

• Tham số Poisson

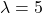
Xác suất để nhận được 7 cuộc gọi trong một giờ sẽ được tính bằng:

Ứng dụng:

Phân phối Poisson có nhiều ứng dụng trong các lĩnh vực khác nhau như:

Một trong những điểm nổi bật của phân phối Poisson là nó mô tả được các sự kiện hiếm gặp. Điều này có nghĩa là trong tình huống mà các sự kiện xảy ra một cách ngẫu nhiên và độc lập, chúng sẽ tuân theo quy luật Poisson. Chẳng hạn, số lần một máy tính bị treo trong một tháng có thể được mô tả bởi phân phối Poisson. Bên cạnh đó, phân phối này không yêu cầu các sự kiện phải xảy ra trong khoảng thời gian cố định, và có thể áp dụng cho các không gian khác nhau.

Với những đặc điểm trên, phân phối Poisson trở thành một công cụ hữu ích trong nhiều lĩnh vực, từ phân tích dữ liệu đến nghiên cứu khoa học và quản lý. Việc hiểu rõ về phân phối Poisson và các tham số của nó chính là chìa khóa để áp dụng hiệu quả trong thực tiễn.

Cuối cùng, diện tích dưới đường cong phân phối Poisson có ý nghĩa sâu sắc trong việc xác định xác suất của một hoặc nhiều sự kiện xảy ra trong một khoảng thời gian nhất định, từ đó giúp cho việc ra quyết định chính xác hơn trong các ứng dụng thực tiễn.

Ứng Dụng của Phân Phối Poisson trong Các Lĩnh Vực Khác Nhau

Phân phối Poisson là một công cụ thống kê mạnh mẽ, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau để mô tả và phân tích các hiện tượng ngẫu nhiên. Trong lĩnh vực khoa học tự nhiên, ví dụ, phân phối này có thể được áp dụng để mô tả số lượng hạt phóng xạ phát ra trong một khoảng thời gian xác định. Điều này rất quan trọng trong việc nghiên cứu chất phóng xạ và có thể giúp các nhà khoa học hiểu rõ hơn về sự phân rã hạt nhân.

Tương tự, trong lĩnh vực kỹ thuật, phân phối Poisson thường được áp dụng để phân tích các sự kiện hỏng hóc trong các hệ thống máy móc. Các kỹ sư có thể sử dụng phân phối này để dự đoán khả năng xảy ra sự cố trong một khoảng thời gian nhất định, điều này giúp họ lên kế hoạch bảo trì và giảm thiểu rủi ro. Việc hiểu rõ số lượng sự cố có thể xảy ra cũng giúp tối ưu hóa chi phí vận hành.

Trong lĩnh vực y tế, phân phối Poisson có thể được sử dụng để mô tả số ca mắc bệnh trong một khoảng thời gian cụ thể. Chẳng hạn, khi nghiên cứu sự lây lan của dịch bệnh, các nhà dịch tễ học có thể sử dụng phân phối này để theo dõi và dự đoán số lượng ca mắc mới. Điều này rất có ích trong việc lập kế hoạch triển khai nguồn lực y tế và ngăn chặn sự bùng phát của các dịch bệnh.

Cuối cùng, trong lĩnh vực kinh doanh, các nhà quản lý có thể áp dụng phân phối Poisson để dự đoán số lượng khách hàng hoặc giao dịch trong một khoảng thời gian nhất định. Việc dự đoán chính xác này giúp doanh nghiệp tối ưu hóa quy trình phục vụ và tăng cường trải nghiệm của khách hàng. Qua đó, phân phối Poisson thật sự trở thành một công cụ hữu ích trong nhiều lĩnh vực khác nhau, hỗ trợ quyết định dựa trên dữ liệu.

Những Hạn Chế của Phân Phối Poisson và Cách Giải Quyết

Phân phối Poisson là một công cụ mạnh mẽ trong thống kê và thường được sử dụng để mô tả số lượng sự kiện diễn ra trong một khoảng thời gian hoặc không gian nhất định. Tuy nhiên, nó cũng có những hạn chế nhất định mà các nhà thống kê và nghiên cứu viên cần lưu ý. Một trong những hạn chế chính của phân phối Poisson là giả định rằng các sự kiện xảy ra độc lập lẫn nhau, điều này không luôn đúng trong thực tế. Khi có sự tương tác giữa các sự kiện, phân phối Poisson có thể dẫn đến kết quả không chính xác.

Thêm vào đó, phân phối này cũng yêu cầu rằng tỷ lệ xảy ra các sự kiện là cố định trong suốt thời gian quan sát. Tuy nhiên, trong nhiều tình huống thực tế, tỷ lệ này có thể thay đổi, ảnh hưởng đến độ chính xác của mô hình. Ví dụ, trong các lĩnh vực như y tế hoặc giao thông, sự biến động tự nhiên có thể dẫn đến việc số lượng sự kiện không phù hợp với những giả định của phân phối Poisson.

Các nhà thống kê thường phải tìm kiếm các giải pháp thay thế khi đối mặt với những hạn chế của phân phối Poisson. Một trong những lựa chọn phổ biến là sử dụng phân phối nhị thức, được áp dụng trong các tình huống mà có một số lượng cố định các thử nghiệm. Ngoài ra, phân phối siêu Poisson cũng có thể được xem xét khi có sự gia tăng trong biến động của các sự kiện. Bằng cách này, nhà nghiên cứu có thể điều chỉnh mô hình của mình để phù hợp hơn với dữ liệu thực tế mà họ đang làm việc.

Cuối cùng, việc hiểu rõ những hạn chế của phân phối Poisson và nhận diện các tình huống không phù hợp sẽ giúp các nhà thống kê có thể áp dụng các phương pháp tiếp cận chính xác hơn, từ đó cải thiện chất lượng của kết quả nghiên cứu.