











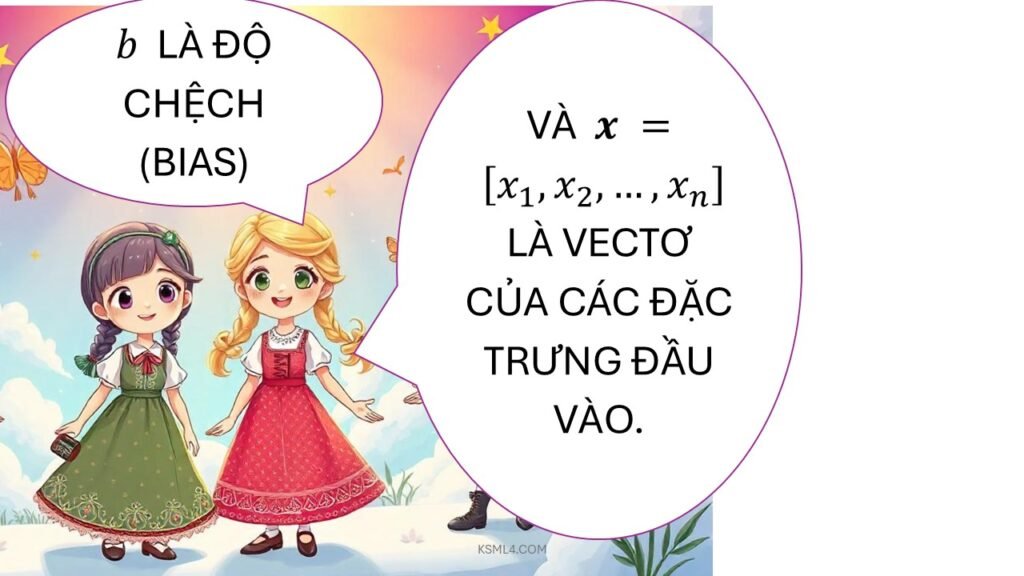



Hồi quy logistic có thể được xây dựng dựa trên phân phối Bernoulli vì đầu ra của bài toán phân loại nhị phân chỉ có hai giá trị: ![]() .
.
🔎 Bước hình thành
- Mô hình Bernoulli cho biến nhãn
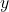 :
:
- Giả sử xác suất để
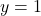 là
là 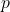 , thì:
, thì:![Rendered by QuickLaTeX.com \[ P(y \mid x) = p^y (1-p)^{1-y}\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-3f5d6026b0226f12e216642594a2a50a_l3.png)
- Đây chính là phân phối Bernoulli.
- Liên hệ xác suất với đặc trưng
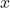 :
:
- Ta muốn mô hình hóa
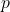 như một hàm của
như một hàm của 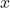 .
. - Dùng hàm logistic (sigmoid):
![Rendered by QuickLaTeX.com \[ p(x) = \sigma(z) = \frac{1}{1+e^{-z}}, \quad z = w^T x + b \]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-b45ce358ab431b49d2a28b2bca8f937c_l3.png)
- Nhờ sigmoid, giá trị
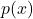 luôn nằm trong khoảng
luôn nằm trong khoảng 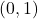 .
.
- Hàm likelihood (khả năng xảy ra):
- Với tập dữ liệu
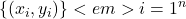 :
: ![Rendered by QuickLaTeX.com \[ L(w) = \prod</em>{i=1}^n p(x_i)^{y_i} \cdot (1-p(x_i))^{1-y_i} \]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-1f7795c09aa87e31768b26f974a5de41_l3.png)
- Hàm log-likelihood:
- Để dễ tính toán, lấy log:
![Rendered by QuickLaTeX.com \[ \ell(w) = \sum_{i=1}^n \Big[ y_i \log p(x_i) + (1-y_i)\log(1-p(x_i)) \Big] \]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-1ef06ae5f5d31b85b9dd471c1a800495_l3.png)
- Ước lượng tham số:
- Tìm
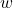 tối ưu bằng cách tối đa hóa log-likelihood (Maximum Likelihood Estimation – MLE).
tối ưu bằng cách tối đa hóa log-likelihood (Maximum Likelihood Estimation – MLE). - Thường dùng Gradient Descent hoặc các biến thể để giải.
🌍 Ý nghĩa
- Hồi quy logistic thực chất là mô hình Bernoulli với xác suất thành công được mô hình hóa bằng hàm sigmoid của đặc trưng đầu vào.
- Nhờ vậy, nó trở thành công cụ mạnh mẽ cho phân loại nhị phân: spam/không spam, bệnh/không bệnh, thắng/thua,…
Discover more from Cùng Học Cùng Mơ
Subscribe to get the latest posts sent to your email.
