13. đạo hàm và tính liên tục

1. Nếu hàm số có đạo hàm tại điểm , thì hàm số chắc chắn liên tục tại .

• Vì đạo hàm tồn tại nghĩa là giới hạn của 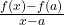tồn tại.
• Điều này kéo theo .

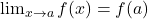1. Chiều ngược lại không đúng:

• Một hàm có thể liên tục tại nhưng không có đạo hàm tại .
• Ví dụ: 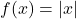liên tục tại 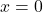, nhưng không có đạo hàm tại 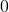vì giới hạn trái và phải khác nhau.

📊 Ví dụ minh họa

Ví dụ 1: Hàm liên tục và có đạo hàm

   

• Liên tục trên .
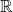• Đạo hàm: .
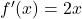  👉 Vừa liên tục vừa khả vi (có đạo hàm) ở mọi điểm.

Ví dụ 2: Hàm liên tục nhưng không khả vi

   

• Liên tục trên .
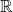• Tại :
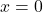• Giới hạn trái củ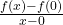a là .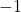
• Giới hạn phải là .
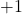  👉 Không có đạo hàm tại .

✨ Tóm lại

Có đạo hàm ⇒ liên tục.
Liên tục ⇏ có đạo hàm.