17. cực trị và điểm bất động

by Kurious Fox

📌 1. Cực trị của hàm số

Định nghĩa: Điểm cực trị là những điểm mà tại đó hàm số đạt giá trị lớn nhất (cực đại) hoặc nhỏ nhất (cực tiểu) trong một vùng lân cận.

Điều kiện cần: Nếu 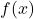$f(x)$ có đạo hàm tại 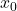$x_0$ , thì để 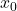$x_0$ là cực trị ta phải có:
$f'(x_0) = 0$
Điều kiện đủ:
Nếu 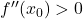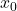$f''(x_0) > 0$ ⇒ $x_0$ là cực tiểu.
Nếu 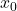$f''(x_0) < 0$ ⇒ $x_0$ là cực đại.
Nếu $f''(x_0) = 0$ ⇒ cần xét thêm.

🔹 Ví dụ:

$f(x) = x^2$

$f'(x) = 2x$ .
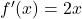Giải $f'(x)=0 \Rightarrow x=0$ .
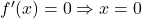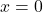$f''(x) = 2 > 0$ ⇒ $x=0$ là cực tiểu.

📌 2. Điểm bất động (Fixed Point)

Định nghĩa: Điểm bất động của hàm số $f(x)$ là nghiệm của phương trình:

$f(x) = x$

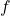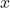Ý nghĩa: Khi áp dụng hàm $f$ lên $x$ , ta thu được chính nó ⇒ điểm đó “không di chuyển”.

🔹 Ví dụ:

$f(x) = \cos x$

Điểm bất động là nghiệm của $\cos x = x$ .
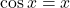Có một nghiệm duy nhất gần 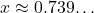$x \approx 0.739…$ (gọi là nghiệm Dottie).

✨ Tóm lại

Cực trị: nơi hàm đạt giá trị lớn nhất hoặc nhỏ nhất cục bộ.
Điểm bất động: nghiệm của phương trình $f(x) = x$ .

Related

Leave a ReplyCancel reply

error: Content is protected !!