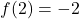Skip to content

18. Cách tìm cực trị

📌 Các bước tìm cực trị của hàm số 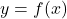y = f(x)

🔹 Bước 1: Tính đạo hàm f'(x)

  • Đây là bước quan trọng để xác định điểm mà hàm có thể đạt cực trị.

🔹 Bước 2: Giải phương trình f'(x) = 0

  • Tìm các nghiệm của phương trình này → gọi là điểm nghi ngờ cực trị.

🔹 Bước 3: Xét dấu đạo hàm hoặc dùng đạo hàm cấp hai

Cách 1: Xét dấu đạo hàm f'(x)

  • Lập bảng biến thiên.
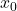  • Nếu f'(x) đổi dấu từ dương → âm tại điểm x_0 ⇒ cực đại.
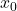  • Nếu f'(x) đổi dấu từ âm → dương tại điểm x_0 ⇒ cực tiểu.

Cách 2: Dùng đạo hàm cấp hai 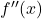f''(x)

  • Nếu 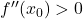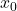f''(x_0) > 0 ⇒ x_0 là cực tiểu.
  • Nếu 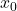f''(x_0) < 0 ⇒ x_0 là cực đại.
  • Nếu f''(x_0) = 0 ⇒ cần xét thêm.

📊 Ví dụ minh họa

Cho hàm:

    \[ f(x) = x^3 - 3x^2 + 2\]

Bước 1:

    \[ f'(x) = 3x^2 - 6x\]

Bước 2:

    \[ f'(x) = 0 \Rightarrow 3x(x - 2) = 0 \Rightarrow x = 0, x = 2\]

Bước 3:

  • f''(x) = 6x - 6
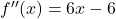
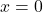  • f''(0) = -6 < 0 ⇒ x=0 là cực đại
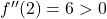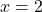  • f''(2) = 6 > 0 ⇒ x=2 là cực tiểu

✨ Kết luận

  • Hàm có cực đại tại 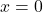x=0, cực tiểu tại x=2.
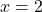  • Giá trị cực đại: 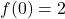f(0) = 2, cực tiểu: f(2) = -2

Leave a Reply

error: Content is protected !!