









phép thử đạo hàm cấp 2 (hay còn gọi là Second Derivative Test) trong giải tích là một công cụ quan trọng để xác định cực trị (cực đại, cực tiểu) của hàm số. Mình sẽ giải thích chi tiết và có ví dụ minh họa nhé:
🔎 Nguyên lý của phép thử đạo hàm cấp 2
Giả sử ta có một hàm số ![]() khả vi đến cấp 2 trên khoảng chứa điểm
khả vi đến cấp 2 trên khoảng chứa điểm ![]() :
:
- Bước 1: Tìm nghiệm của đạo hàm cấp 1
- Giải phương trình
 .
. - Các nghiệm
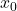 gọi là điểm tới hạn (critical points).
gọi là điểm tới hạn (critical points).
- Bước 2: Xét đạo hàm cấp 2 tại điểm tới hạn
- Nếu
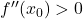 → hàm số lõm lên tại
→ hàm số lõm lên tại 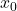 , nên
, nên 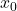 là cực tiểu địa phương.
là cực tiểu địa phương. - Nếu
 → hàm số lõm xuống tại
→ hàm số lõm xuống tại 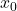 , nên
, nên 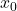 là cực đại địa phương.
là cực đại địa phương. - Nếu
 → phép thử không kết luận được, cần dùng phương pháp khác (ví dụ: xét đạo hàm cao hơn hoặc dùng phép thử đạo hàm cấp 1).
→ phép thử không kết luận được, cần dùng phương pháp khác (ví dụ: xét đạo hàm cao hơn hoặc dùng phép thử đạo hàm cấp 1).
📘 Ví dụ minh họa
Xét hàm số:
![]()
Bước 1: Tính đạo hàm cấp 1
![]()
⇒ nghiệm:
Bước 2: Tính đạo hàm cấp 2
![]()
- Tại
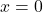 :
:  ⇒ cực đại địa phương.
⇒ cực đại địa phương. - Tại
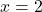 :
: 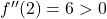 ⇒ cực tiểu địa phương.
⇒ cực tiểu địa phương.
🎯 Tóm lại
- Phép thử đạo hàm cấp 2 giúp ta nhanh chóng xác định loại cực trị tại điểm tới hạn.
- Nó dựa vào độ cong (concavity) của đồ thị hàm số.
- Nếu đạo hàm cấp 2 bằng 0 thì phải dùng phương pháp khác để kiểm tra.
📊 Ví dụ:
Cho hàm số:
![]()
🔹 Bước 1: Tính đạo hàm
![]()
🔹 Bước 2: Giải phương trình 
![]()
👉 Đây là hai điểm nghi ngờ cực trị.
🔹 Bước 3: Dùng đạo hàm cấp hai
![]()
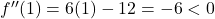 ⇒
⇒ 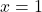 là cực đại
là cực đại ⇒
⇒ 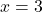 là cực tiểu
là cực tiểu
🔹 Bước 4: Tính giá trị cực trị
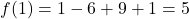 ⇒ Cực đại tại (1, 5)
⇒ Cực đại tại (1, 5)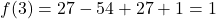 ⇒ Cực tiểu tại (3, 1)
⇒ Cực tiểu tại (3, 1)
✅ Kết luận
- Cực đại: tại
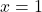 , giá trị
, giá trị 
- Cực tiểu: tại
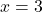 , giá trị
, giá trị 
