










📌 1. Hàm số là gì?
- Hàm số là một quy tắc gán mỗi giá trị của biến độc lập (x) với một giá trị duy nhất của biến phụ thuộc (y).
- Ví dụ:
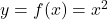 . Với mỗi
. Với mỗi 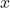 , ta có đúng một giá trị
, ta có đúng một giá trị 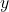 .
.
📌 2. Miền xác định (Domain)
- Miền xác định của hàm số là tập hợp tất cả các giá trị của biến x mà hàm số có nghĩa.
- Cách tìm miền xác định:
- Với phân số: mẫu số ≠ 0.
- Với căn bậc chẵn: biểu thức trong căn ≥ 0.
- Với logarit: biểu thức trong log > 0.
- Ví dụ:
- Hàm
 có miền xác định:
có miền xác định: 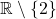 .
. - Hàm
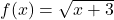 có miền xác định:
có miền xác định:  .
.
📌 3. Miền giá trị (Range)
- Miền giá trị là tập hợp tất cả các giá trị y = f(x) mà hàm số có thể nhận khi x chạy trong miền xác định.
- Ví dụ:
- Hàm
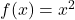 có miền giá trị:
có miền giá trị:  .
. - Hàm
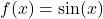 có miền giá trị:
có miền giá trị: ![Rendered by QuickLaTeX.com [-1, 1]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-61888feeeeb8e122a17b229740cd3b65_l3.png) .
.
📊 Tóm tắt
| Khái niệm | Ý nghĩa | Ví dụ |
|---|---|---|
| Hàm số | Quy tắc gán mỗi x → một y duy nhất | |
| Miền xác định | Tập hợp giá trị x để hàm có nghĩa | |
| Miền giá trị | Tập hợp giá trị y mà hàm nhận được |
Tuyệt vời 👌. Mình sẽ lấy một ví dụ cụ thể để bạn thấy rõ cách tìm miền xác định và miền giá trị nhé.
Ví dụ: 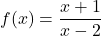
🔹 Miền xác định
- Điều kiện: mẫu số ≠ 0
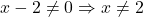
👉 Vậy miền xác định: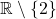
🔹 Miền giá trị
Ta xét ![]() .
.
- Biến đổi:
![Rendered by QuickLaTeX.com \[ y = \dfrac{x+1}{x-2} \quad \Rightarrow \quad y(x-2) = x+1 \]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-6bc914d8be08580f0438f1603f13acac_l3.png)
![Rendered by QuickLaTeX.com \[ \Rightarrow yx - 2y = x + 1 \quad \Rightarrow \quad x(y-1) = 2y + 1 \]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-6813ca1e523bd0efb1d5023308427cf8_l3.png)
![Rendered by QuickLaTeX.com \[ \Rightarrow x = \dfrac{2y+1}{y-1}, \quad y \neq 1 \]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-5656602e923d05bdebf623d2a32fb3f0_l3.png)
- Như vậy, với mọi
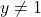 , ta đều tìm được
, ta đều tìm được 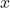 thỏa mãn.
thỏa mãn.
👉 Miền giá trị: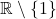
📊 Tóm lại
- Miền xác định:
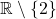
- Miền giá trị:
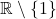
Ví dụ: 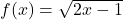
🔹 Miền xác định
- Điều kiện: Biểu thức trong căn phải ≥ 0
![Rendered by QuickLaTeX.com \[ 2x - 1 \geq 0 \quad \Rightarrow \quad x \geq \tfrac{1}{2}\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-01ae96ea345b135371114047afa4f987_l3.png)
👉 Vậy miền xác định: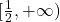
🔹 Miền giá trị
- Với
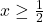 , ta có
, ta có 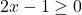 .
. - Khi đó
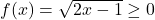 .
. - Giá trị nhỏ nhất: khi
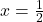 , ta được
, ta được 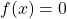 .
. - Khi
 , thì
, thì  .
.
👉 Vậy miền giá trị: ![]()
📊 Tóm lại
- Miền xác định:
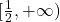
- Miền giá trị:

Ví dụ: 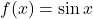
🔹 Miền xác định
- Hàm số lượng giác
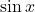 được xác định với mọi số thực.
được xác định với mọi số thực.
👉 Miền xác định: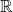
🔹 Miền giá trị
- Với mọi
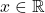 , ta có
, ta có 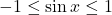 .
.
👉 Miền giá trị:![Rendered by QuickLaTeX.com [-1, 1]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-61888feeeeb8e122a17b229740cd3b65_l3.png)
📊 Tóm lại
- Miền xác định:
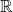
- Miền giá trị:
![Rendered by QuickLaTeX.com [-1, 1]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-61888feeeeb8e122a17b229740cd3b65_l3.png)
