








📌 Định lý (Quy tắc chuỗi)
Nếu ta có hàm hợp:
![]()
với ![]() khả vi và
khả vi và ![]() khả vi (trong đó
khả vi (trong đó ![]() ), thì đạo hàm của
), thì đạo hàm của ![]() theo
theo ![]() là:
là:
![]()
👉 Nói ngắn gọn: đạo hàm của hàm hợp = đạo hàm bên ngoài × đạo hàm bên trong.
📊 Ví dụ minh họa
Ví dụ 1:
![]()
- Đặt
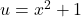 .
. - Khi đó
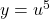 .
. - Đạo hàm:
![Rendered by QuickLaTeX.com \[ \frac{dy}{dx} = 5u^4 \cdot \frac{du}{dx} = 5(x^2+1)^4 \cdot (2x)\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-3b1d72d7298e6fd2f6d342710cee7094_l3.png)
- Kết quả:
![Rendered by QuickLaTeX.com \[ y' = 10x(x^2+1)^4\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-0ca904fb76927d1fbd6ba5eb2150fe5a_l3.png)
Ví dụ 2:
![]()
- Hàm ngoài:
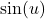 , đạo hàm là
, đạo hàm là 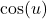 .
. - Hàm trong:
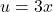 , đạo hàm là
, đạo hàm là 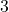 .
. - Kết quả:
![Rendered by QuickLaTeX.com \[ y' = \cos(3x) \cdot 3 = 3\cos(3x)\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-03a32923ce46ad2ebd349649f4879f3a_l3.png)
✨ Ý nghĩa
- Quy tắc chuỗi cho phép ta xử lý hàm lồng nhau.
- Đây là nền tảng để tính đạo hàm trong các bài toán phức tạp (ví dụ hàm mũ, logarit, lượng giác lồng nhau).
📊 Ví dụ 3:
![]()
Bước 1: Xác định hàm ngoài và hàm trong
- Hàm ngoài:
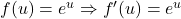
- Hàm trong:
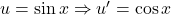
Bước 2: Áp dụng quy tắc chuỗi
![]()
👉 Kết quả:
![]()
📊 Ví dụ 4:
![]()
Bước 1:
- Hàm ngoài:
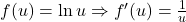
- Hàm trong:
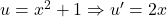
Bước 2:
![]()
👉 Kết quả:
![]()
