22. đạo hàm hàm hợp

by Kurious Fox

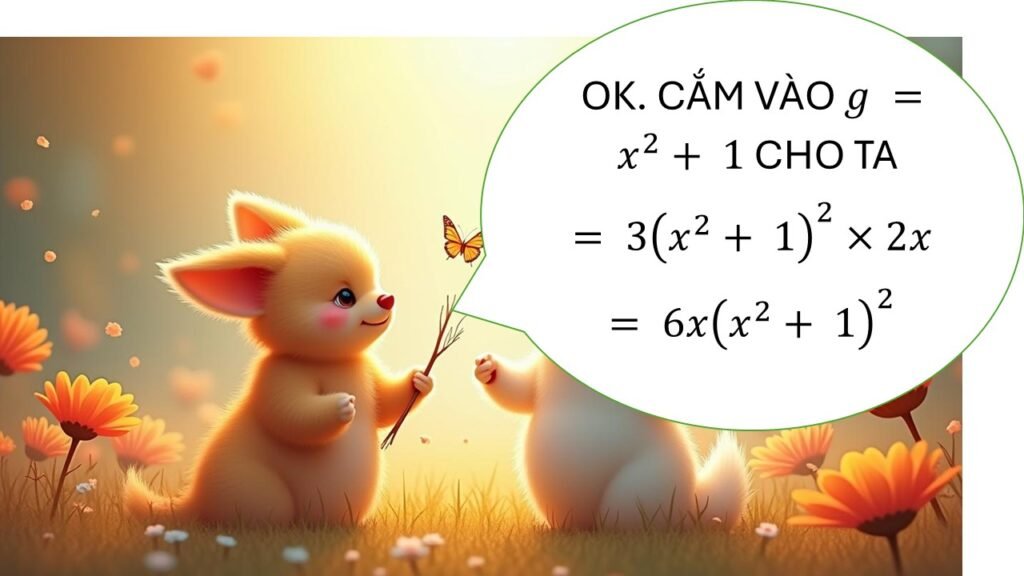
📌 Định nghĩa

Cho hàm hợp:

$y = f(g(x))$

Nếu $g(x)$ khả vi và $f(u)$ khả vi (với $u = g(x)$ ), thì đạo hàm của $y$ theo $x$ là:

$\frac{dy}{dx} = f'(g(x)) \cdot g'(x)$

👉 Nói ngắn gọn: đạo hàm ngoài × đạo hàm trong.

📊 Ví dụ minh họa

Ví dụ 1:

$y = (x^2 + 1)^5$

Hàm ngoài: $f(u) = u^5 \Rightarrow f'(u) = 5u^4$
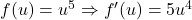
Hàm trong: $u = x^2+1 \Rightarrow u' = 2x$
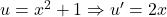
Kết quả:
$y' = 5(x^2+1)^4 \cdot 2x = 10x(x^2+1)^4$

Ví dụ 2:

$y = \sin(3x)$

Hàm ngoài: $f(u) = \sin u \Rightarrow f'(u) = \cos u$
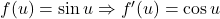
Hàm trong: $u = 3x \Rightarrow u' = 3$
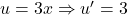
Kết quả:
$y' = \cos(3x) \cdot 3 = 3\cos(3x)$

Ví dụ 3:

$y = \ln(\cos x)$

Hàm ngoài: $f(u) = \ln u \Rightarrow f'(u) = \frac{1}{u}$
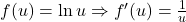
Hàm trong: $u = \cos x \Rightarrow u' = -\sin x$
Kết quả:
$y' = \frac{1}{\cos x} \cdot (-\sin x) = -\tan x$

Related

Discover more from Cùng Học Cùng Mơ

Subscribe to get the latest posts sent to your email.

Leave a ReplyCancel reply

error: Content is protected !!