







📌 Ứng dụng trong toán học
- Tính đạo hàm của hàm phức tạp
- Khi gặp biểu thức lồng nhau (ví dụ
 ,
, 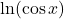 ,
,  ), quy tắc chuỗi giúp ta tính nhanh mà không cần biến đổi dài dòng.
), quy tắc chuỗi giúp ta tính nhanh mà không cần biến đổi dài dòng.
- Giải phương trình cực trị
- Nhiều hàm số thực tế có dạng hợp, ví dụ
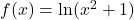 .
. - Muốn tìm cực trị, ta phải tính đạo hàm bằng quy tắc chuỗi.
- Tính đạo hàm trong tích phân đổi biến
- Khi đổi biến trong tích phân, quy tắc chuỗi xuất hiện tự nhiên để tính đạo hàm của biến mới.
📊 Ứng dụng trong thực tế
🔹 Vật lý
Chuyển động phức tạp: Vận tốc là đạo hàm của quãng đường theo thời gian. Nếu quãng đường được mô tả bằng hàm hợp (ví dụ ![]() ), ta dùng quy tắc chuỗi để tính vận tốc.
), ta dùng quy tắc chuỗi để tính vận tốc.
![]()
🔹 Kinh tế
Tốc độ tăng trưởng: Nếu lợi nhuận phụ thuộc vào giá trị đầu tư, mà giá trị đầu tư lại phụ thuộc vào thời gian, thì đạo hàm hàm hợp cho ta tốc độ thay đổi lợi nhuận theo thời gian.
🔹 Sinh học
Mô hình tăng trưởng quần thể: Quần thể có thể phụ thuộc vào nhiệt độ, mà nhiệt độ lại phụ thuộc vào thời gian. Đạo hàm hàm hợp giúp mô tả tốc độ biến đổi quần thể theo thời gian.
✨ Ví dụ minh họa
Giả sử quãng đường đi được của một vật:
![]()
- Vận tốc:
![Rendered by QuickLaTeX.com \[ v(t) = \frac{ds}{dt} = e^{\sin t} \cdot \cos t\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-65a768126a794c75b627521b9467549e_l3.png)
👉 Đây là ứng dụng trực tiếp của quy tắc chuỗi trong vật lý.
📌 Tóm lại: Đạo hàm hàm hợp là công cụ bắt buộc khi mô tả tốc độ biến đổi của các hệ thống phức tạp — từ toán học thuần túy đến vật lý, kinh tế, sinh học.
