





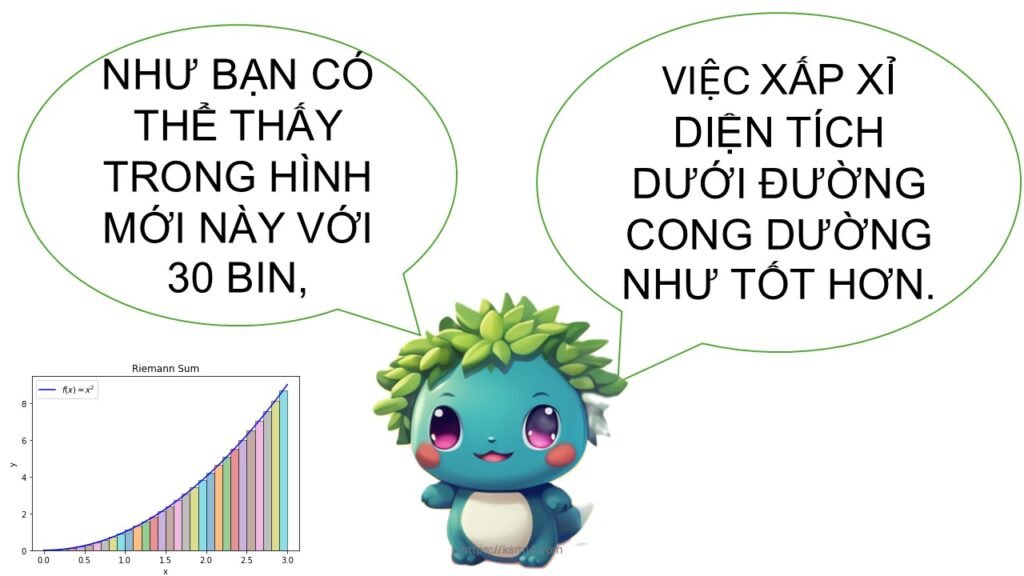

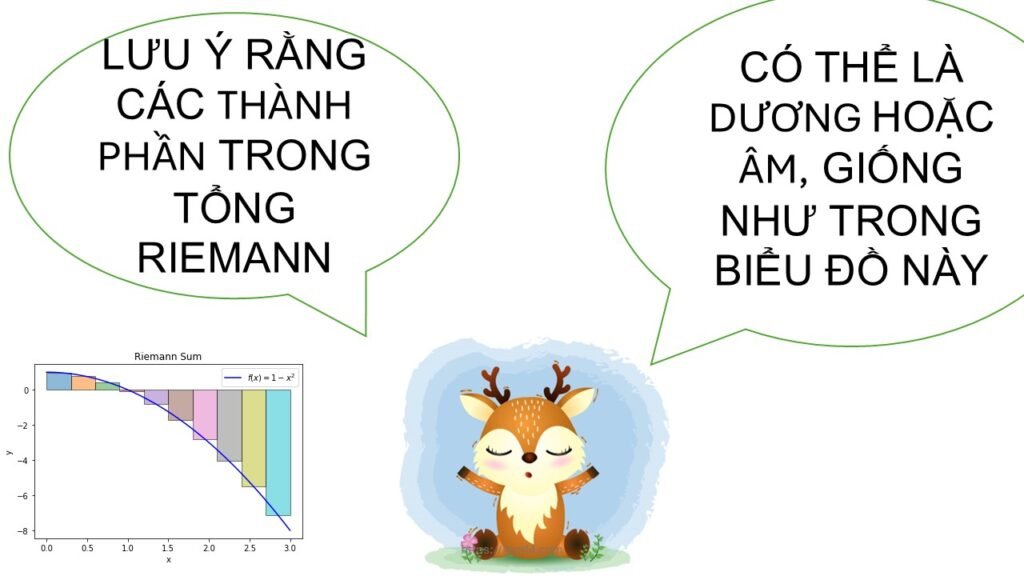
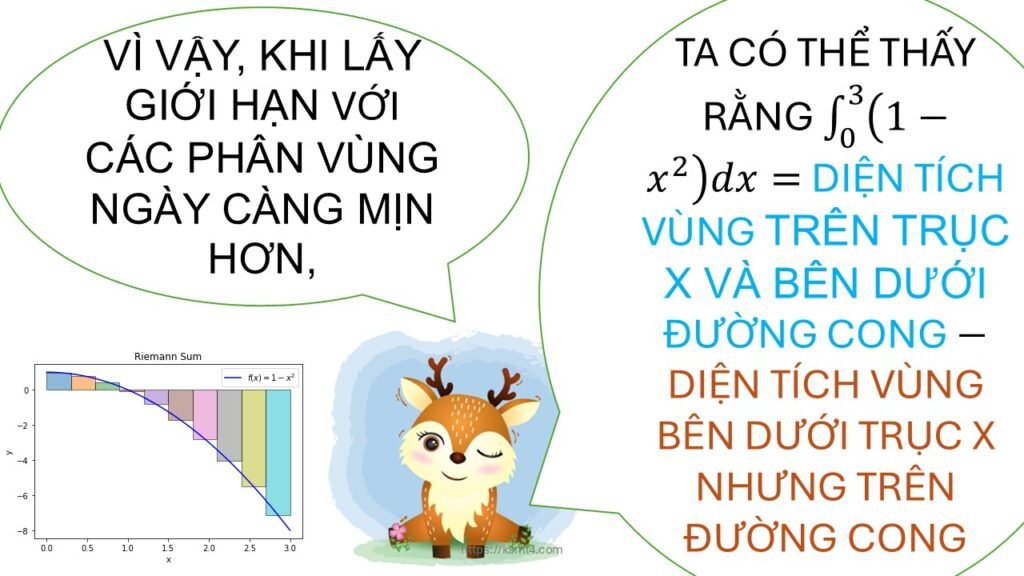
📌 Định nghĩa
Tích phân bất định: là phép toán ngược của đạo hàm.
Nếu ![]() , thì:
, thì:
![]()
(trong đó
📊 Ví dụ minh họa
Ví dụ 1: Tích phân bất định
![]()
👉 Vì đạo hàm của ![]() là
là ![]() .
.
📊 Ví dụ minh họa
Ví dụ 1:
![]()
- Nguyên hàm của
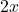 là
là 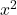 .
. - Kết quả:
![Rendered by QuickLaTeX.com \[ \int 2x \, dx = x^2 + C\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-fe2c38470cdadac281c0fffa9474bfa5_l3.png)
Ví dụ 2:
![]()
- Nguyên hàm của
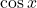 là
là 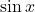 .
. - Kết quả:
![Rendered by QuickLaTeX.com \[ \int \cos x \, dx = \sin x + C\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-399317ebc9f28a4099a378000d4b2b16_l3.png)
Ví dụ 3:
![]()
- Nguyên hàm của
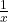 là
là 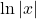 .
. - Kết quả:
![Rendered by QuickLaTeX.com \[ \int \frac{1}{x} \, dx = \ln |x| + C\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-19470d83b5460fd8de38265413dfef7d_l3.png)
Ví dụ 4:
![]()
- Nguyên hàm của
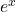 là chính nó.
là chính nó. - Kết quả:
![Rendered by QuickLaTeX.com \[ \int e^x \, dx = e^x + C\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-c091e99feb181b4f61020200106376c2_l3.png)
✨ Nhận xét
- Tích phân bất định giúp ta tìm nguyên hàm của một hàm số.
- Đây là bước quan trọng để giải các bài toán về diện tích, thể tích, và ứng dụng trong vật lý, kinh tế.
