Chuyển tới nội dung

25. tích phân không xác định

Tích phân không xác định (indefinite integral) chính là nguyên hàm của một hàm số, ký hiệu \int f(x)\,dx = F(x) + C, trong đó F'(x) = f(x) và C là hằng số tùy ý.

📘 Khái niệm cơ bản

Định nghĩa: Tích phân không xác định của hàm f(x) là tập hợp tất cả các nguyên hàm của f(x).

    \[ \int f(x)\,dx = F(x) + C\]


với F'(x) = f(x).
Khác biệt với tích phân xác định:

  • Tích phân không xác định → cho ra một hàm (nguyên hàm).
  • Tích phân xác định → cho ra một số (diện tích dưới đường cong).

🔑 Tính chất quan trọng

  • Tuyến tính:

        \[ \int \big(f(x) + g(x)\big)\,dx = \int f(x)\,dx + \int g(x)\,dx\]


        \[ \int k \cdot f(x)\,dx = k \cdot \int f(x)\,dx\]

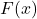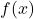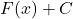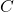  • Nếu F(x) là một nguyên hàm của f(x), thì mọi hàm F(x) + C (với C bất kỳ) cũng là nguyên hàm của f(x).

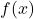📐 Một số công thức cơ bản

  • \int dx = x + C
  • \int x^n dx = \frac{x^{n+1}}{n+1} + C \quad (n \neq -1)
  • \int \frac{1}{x} dx = \ln|x| + C
  • \int e^x dx = e^x + C
  • \int \sin x dx = -\cos x + C
  • \int \cos x dx = \sin x + C

🌟 Ví dụ minh họa

  1. \int (2x + 3)\,dx = x^2 + 3x + C
  2. \int \cos x\,dx = \sin x + C
  3. \int \frac{1}{x}\,dx = \ln|x| + C

🎯 Ứng dụng

  • Tìm hàm gốc từ đạo hàm (ví dụ trong vật lý: từ vận tốc tìm vị trí).
  • Giải phương trình vi phân.
  • Là bước trung gian để tính tích phân xác định (diện tích, thể tích, công, xác suất…).

Gửi phản hồi

error: Content is protected !!