3. Vẽ đồ thị hàm số

by Kurious Fox

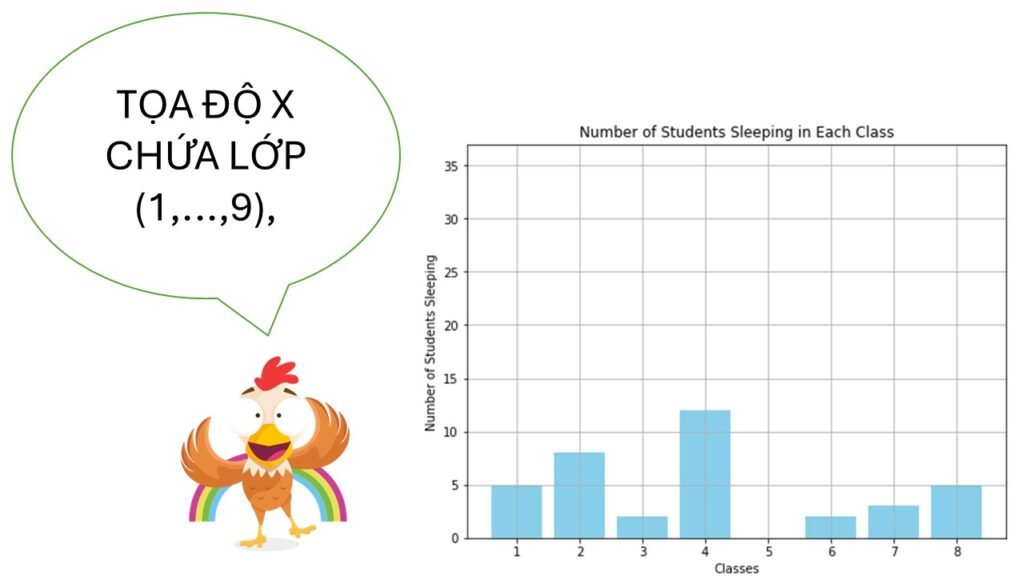
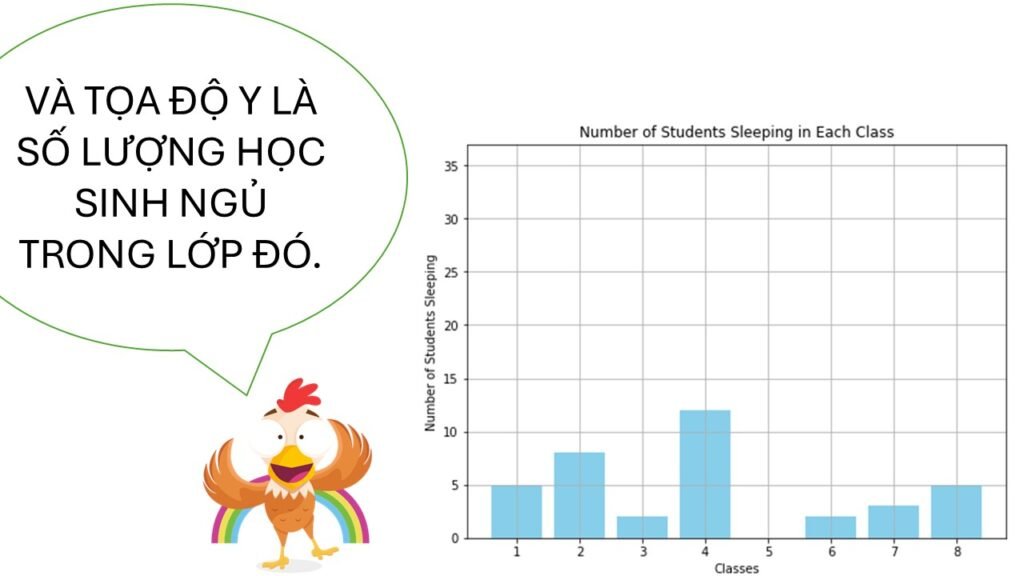
📌 Các bước vẽ đồ thị hàm số

1. Xác định miền xác định

Tìm tất cả giá trị 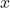$x$ mà hàm số có nghĩa (loại bỏ mẫu số bằng 0, căn bậc chẵn âm, logarit ≤ 0…).
Đây là tập giá trị mà ta sẽ xét khi vẽ đồ thị.

2. Tìm miền giá trị (nếu cần)

Giúp hình dung phạm vi 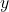$y$ mà đồ thị có thể đạt được.
Ví dụ: $\sin x \in [-1,1]$ .

3. Xét tính chất của hàm số

Tập xác định: đã tìm ở bước 1.
Tính chẵn/lẻ:

Nếu 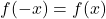$f(-x) = f(x)$ → hàm chẵn → đồ thị đối xứng qua trục $Oy$ .
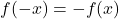Nếu $f(-x) = -f(x)$ → hàm lẻ → đồ thị đối xứng qua gốc tọa độ.
Chu kỳ (với lượng giác).
Giới hạn: xét khi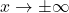 $x \to \pm \infty$ hoặc gần điểm loại trừ.
Tiệm cận: ngang, đứng, xiên (nếu có).

4. Tính đạo hàm để khảo sát

$f'(x)$ : xét dấu để biết hàm đồng biến/ nghịch biến.
Cực trị: nghiệm của $f'(x) = 0$ .
$f''(x)$ : xét độ cong, tìm điểm uốn.

5. Lập bảng biến thiên

Ghi lại các khoảng tăng/giảm, cực trị, tiệm cận.
Đây là “bản đồ” để vẽ đồ thị.

6. Vẽ đồ thị

Dựa vào bảng biến thiên, đối xứng, tiệm cận.
Đặt một số điểm đặc biệt (ví dụ: giao với trục $Ox, Oy$ ).
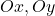Nối các điểm theo chiều biến thiên, chú ý độ cong.

📊 Ví dụ minh họa: 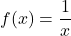$f(x) = \dfrac{1}{x}$

Miền xác định: $\mathbb{R} \setminus \{0\}$ .
Miền giá trị: $\mathbb{R} \setminus \{0\}$ .
Hàm lẻ → đối xứng qua gốc tọa độ.
Tiệm cận đứng: $x=0$ .
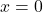Tiệm cận ngang: $y=0$ .
Đồ thị gồm 2 nhánh hyperbol đối xứng.

Related

Leave a ReplyCancel reply

error: Content is protected !!