







📌 Định lý cơ bản
Nếu ![]() có giới hạn khi
có giới hạn khi ![]() , và
, và ![]() là một hằng số, thì:
là một hằng số, thì:
![]()
🔹 Ý nghĩa
- Ta có thể đưa hằng số ra ngoài dấu giới hạn.
- Điều này giúp tính toán nhanh hơn, vì chỉ cần tìm giới hạn của hàm số, rồi nhân với hằng số.
📊 Ví dụ minh họa
Ví dụ 1:
![]()
Ví dụ 2:
![]()
Ví dụ:
![]()
🔹 Bước 1: Tách hằng số ra ngoài
![]()
🔹 Bước 2: Tính giới hạn của 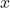 khi
khi 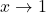
![]()
🔹 Bước 3: Nhân kết quả
![]()
📊 Kết quả
![]()
Ví dụ:
![]()
🔹 Bước 1: Tách hằng số ra ngoài
![]()
🔹 Bước 2: Tính giới hạn của 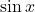 khi
khi 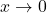
![]()
🔹 Bước 3: Nhân kết quả
![]()
📊 Kết quả
![]()
