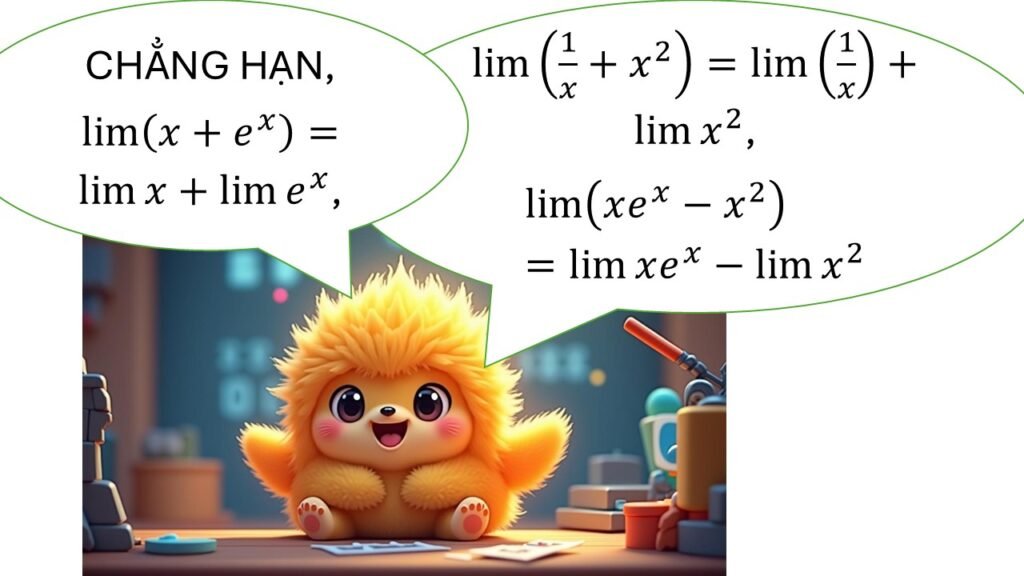
📌 Định lý cơ bản
Nếu 
và 
đều tồn tại, thì:
![\[ \lim_{x \to a} \big(f(x) + g(x)\big) = \lim_{x \to a} f(x) + \lim_{x \to a} g(x)\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-afe45d313044b5a4c0868c3811fb99d5_l3.png "Rendered by QuickLaTeX.com")
🔹 Ý nghĩa
- Ta có thể tách giới hạn của tổng thành tổng các giới hạn.
- Quy tắc này giúp tính toán nhanh hơn, vì chỉ cần tính riêng từng giới hạn rồi cộng lại.
📊 Ví dụ minh họa
Ví dụ 1:
![\[ \lim_{x \to 2} \big(x^2 + 3x\big)= \lim_{x \to 2} x^2 + \lim_{x \to 2} 3x\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-25a42ab86932c448a0e029e70d5540d6_l3.png "Rendered by QuickLaTeX.com")
👉 Kết quả: 
Ví dụ 2:
![\[ \lim_{x \to 0} \big(\sin x + \cos x\big)= \lim_{x \to 0} \sin x + \lim_{x \to 0} \cos x\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-db7c839ff09b1d9eb62dff8d744f2cc1_l3.png "Rendered by QuickLaTeX.com")
👉 Kết quả: 
✨ Như vậy, quy tắc này rất đơn giản: giới hạn của tổng = tổng các giới hạn.