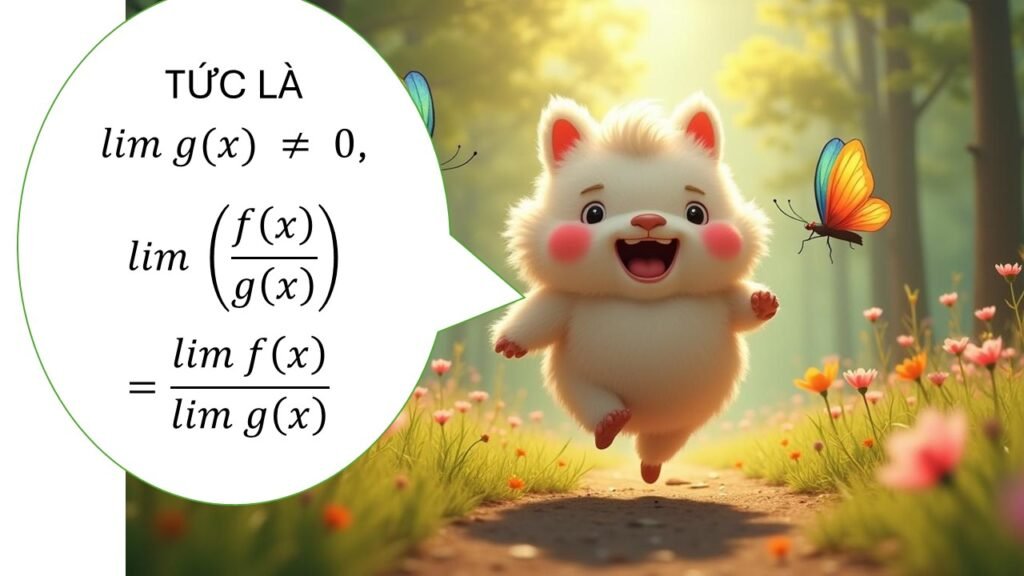
📌 Định lý cơ bản
Nếu 
và 
đều tồn tại, với 
, thì:
![\[ \lim_{x \to a} \frac{f(x)}{g(x)} = \frac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)}\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-646443f21b2becaa65e60bec949e12d4_l3.png "Rendered by QuickLaTeX.com")
🔹 Ý nghĩa
- Ta có thể tách giới hạn của thương thành thương các giới hạn.
- Điều kiện quan trọng: mẫu số không được tiến về 0 (nếu tiến về 0 thì phải xét dạng vô định).
📊 Ví dụ minh họa
Ví dụ 1:
![\[ \lim_{x \to 1} \frac{x^2 + 3}{x+1}= \frac{\lim_{x \to 1} (x^2+3)}{\lim_{x \to 1} (x+1)}\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-4abe17536078fed03c9f61f8386dbbb0_l3.png "Rendered by QuickLaTeX.com")
👉 Kết quả: 
Ví dụ 2 (dạng đặc biệt):
![\[ \lim_{x \to 0} \frac{\sin x}{x}\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-8de3a53088ef550be6dc6de9f6d55a1b_l3.png "Rendered by QuickLaTeX.com")
- Đây là dạng vô định
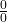. - Kết quả nổi tiếng:
![\[ \lim_{x \to 0} \frac{\sin x}{x} = 1\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-153c09d547a36a10f11bbffc81495ed2_l3.png "Rendered by QuickLaTeX.com")
✨ Như vậy, quy tắc này rất đơn giản: giới hạn của thương = thương các giới hạn, miễn là mẫu số không tiến về 0.