







📌 Nội dung định lý kẹp
Giả sử ta có ba hàm số ![]() xác định trên một khoảng chứa điểm
xác định trên một khoảng chứa điểm ![]() (trừ có thể tại
(trừ có thể tại ![]() ), và thỏa mãn:
), và thỏa mãn:
![]()
![]()
Nếu:
![]()
thì:
![]()
🔹 Ý nghĩa
- Nếu một hàm
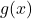 bị “kẹp” giữa hai hàm
bị “kẹp” giữa hai hàm 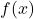 và
và 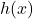 , và cả hai hàm này đều có cùng giới hạn tại điểm
, và cả hai hàm này đều có cùng giới hạn tại điểm  , thì hàm
, thì hàm 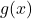 cũng có giới hạn bằng giá trị đó.
cũng có giới hạn bằng giá trị đó. - Đây là công cụ rất mạnh để chứng minh giới hạn của những hàm khó tính trực tiếp.
📊 Ví dụ kinh điển
![]()
- Ta biết:
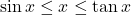 khi
khi 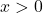 gần 0.
gần 0. - Chia cả ba vế cho
 :
:![Rendered by QuickLaTeX.com \[ \cos x \leq \frac{\sin x}{x} \leq 1\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-ed94f6a96cdc685ecab17e6d33d4a739_l3.png)
- Khi
 :
: 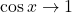 .
.
👉 Vậy theo định lý kẹp:![Rendered by QuickLaTeX.com \[ \lim_{x \to 0} \frac{\sin x}{x} = 1\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-153c09d547a36a10f11bbffc81495ed2_l3.png)
✨ Tóm lại
- Định lý kẹp giúp ta chứng minh giới hạn bằng cách so sánh với hai hàm khác.
- Rất hữu ích cho các giới hạn đặc biệt, đặc biệt trong lượng giác.
Ví dụ:
![]()
🔹 Bước 1: Xét hàm số
- Ta biết
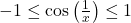 .
.
🔹 Bước 2: Nhân với 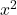
![]()
🔹 Bước 3: Tính giới hạn hai hàm biên
🔹 Bước 4: Áp dụng định lý kẹp
Vì ![]() bị kẹp giữa
bị kẹp giữa ![]() và
và ![]() , và cả hai đều có giới hạn bằng 0 khi
, và cả hai đều có giới hạn bằng 0 khi ![]() , nên:
, nên:
![]()
✨ Kết quả
![]()
