9.biến cố độc lập

Biến cố độc lập là hai biến cố mà việc xảy ra của một biến cố không ảnh hưởng đến xác suất xảy ra của biến cố kia. Đây là khái niệm quan trọng trong xác suất thống kê, giúp phân tích các sự kiện xảy ra một cách riêng biệt.

📘 Định nghĩa chính xác

Hai biến cố và được gọi là độc lập nếu:

   

Nghĩa là xác suất xảy ra đồng thời của A và B bằng tích xác suất riêng của từng biến cố.

🎲 Ví dụ minh họa

Ví dụ 1: Tung hai đồng xu

• Biến cố A: đồng xu thứ nhất ra mặt ngửa →
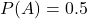
• Biến cố B: đồng xu thứ hai ra mặt ngửa →

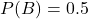
👉 Vì hai lần tung là độc lập, nên:

   

Ví dụ 2: Chọn thẻ và tung xúc xắc

• Biến cố A: rút được thẻ đỏ từ bộ bài
• Biến cố B: xúc xắc ra số chẵn

👉 Hai hành động không liên quan → A và B là độc lập

🧠 Ứng dụng thực tế

Phân tích rủi ro: Xác định các sự cố xảy ra độc lập trong hệ thống
Mô hình hóa thống kê: Dự đoán hành vi người dùng, kết quả khảo sát
Kỹ thuật: Tính xác suất hỏng hóc của các bộ phận không liên quan
Kinh tế học: Phân tích các yếu tố thị trường không ảnh hưởng lẫn nhau

🔍 Cách kiểm tra biến cố độc lập

Để kiểm tra A và B có độc lập không, ta so sánh:

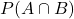• với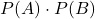
• Nếu bằng nhau → độc lập
• Nếu khác nhau → phụ thuộc

⚠️ 1. Phân tích rủi ro (Risk Analysis)

Tình huống: Một hệ thống máy chủ có 3 ổ cứng hoạt động độc lập.

• Xác suất một ổ cứng bị lỗi trong 1 năm là 0.1
• Ta cần tính xác suất ít nhất một ổ cứng bị lỗi

Ứng dụng biến cố độc lập:

• Gọi A, B, C là biến cố “ổ cứng 1, 2, 3 bị lỗi”
• Vì các ổ cứng hoạt động độc lập, ta tính xác suất không có ổ nào lỗi:
  P( không lỗi)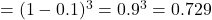
• Vậy xác suất ít nhất một ổ bị lỗi:
  

     

📊 2. Mô hình hóa thống kê (Statistical Modeling)

Tình huống: Một công ty khảo sát hành vi người dùng về hai sản phẩm A và B.

• Xác suất người dùng thích A: 0.6
• Xác suất người dùng thích B: 0.5
• Nếu hai sản phẩm không liên quan về chức năng → biến cố độc lập

Ứng dụng:

• Xác suất người dùng thích cả hai:
  

     

Điều này giúp công ty dự đoán tỷ lệ người dùng tiềm năng cho gói sản phẩm kết hợp.

🔧 3. Kỹ thuật (Engineering)

Tình huống: Một máy móc có 2 bộ phận hoạt động độc lập: động cơ và cảm biến.

• Xác suất động cơ hỏng trong 1 năm: 0.05
• Xác suất cảm biến hỏng: 0.02

Ứng dụng:

• Xác suất cả hai cùng hỏng:
  P( hỏng cả hai)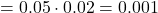
• Xác suất hệ thống vẫn hoạt động (ít nhất một bộ phận còn tốt):
  

     

Giúp kỹ sư đánh giá độ tin cậy của hệ thống.

💰 4. Kinh tế học (Economics)

Tình huống: Phân tích hai yếu tố thị trường:

• A: Giá dầu tăng
• B: Lãi suất ngân hàng thay đổi

Nếu hai yếu tố này không ảnh hưởng trực tiếp đến nhau trong ngắn hạn → biến cố độc lập

Ứng dụng:

• Dự báo xác suất đồng thời xảy ra hai biến động:
  

     

Điều này giúp nhà đầu tư đánh giá rủi ro kép và xây dựng chiến lược phòng ngừa.