phân phối nhị thức là một loại phân phối xác suất rời rạc. Nó mô tả số lần thành công trong một loạt các thử nghiệm độc lập, mỗi thử nghiệm có hai kết quả có thể xảy ra: thành công hoặc thất bại. Phân phối nhị thức thường được sử dụng trong các tình huống mà kết quả của mỗi thử nghiệm chỉ có thể là một trong hai kết quả có thể xảy ra (ví dụ: đúng hoặc sai, có hoặc không).
Các đặc điểm chính của phân phối nhị thức:
- Số lần thử (n): Số lần thử nghiệm được thực hiện.
- Xác suất thành công (p): Xác suất thành công trong mỗi lần thử.
- Xác suất thất bại (q): Xác suất thất bại trong mỗi lần thử, được tính bằng
.
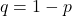Hàm xác suất (PMF):
Hàm xác suất của phân phối nhị thức được cho bởi:
trong đó:
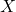là số lần thành công.
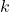là số lần thành công cần tính xác suất.
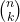là tổ hợp chập k của n.
Kỳ vọng và phương sai:
- Kỳ vọng (mean):
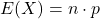
- Phương sai (variance):
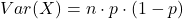
Ví dụ:
Giả sử bạn có một đồng xu cân đối và bạn ném đồng xu 10 lần. Bạn muốn biết xác suất để đồng xu ra mặt ngửa 6 lần. Trong trường hợp này:
- Số lần thử nghiệm
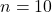
- Xác suất thành công
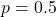(đồng xu cân đối) - Xác suất thất bại
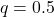
Xác suất để có được 6 lần mặt ngửa trong 10 lần ném sẽ được tính bằng:
Ứng dụng:
Phân phối nhị thức có nhiều ứng dụng trong các lĩnh vực khác nhau như:
- Thống kê: Để xác định xác suất của các sự kiện nhị thức.
- Khoa học xã hội: Để mô hình hóa các khảo sát và thử nghiệm.
- Y học: Để tính toán xác suất thành công của các phương pháp điều trị.
Cụ thể hơn, trong thống kê, phân phối nhị thức thường được sử dụng để đánh giá kết quả của các khảo sát ý kiến hay các cuộc thí nghiệm. Ví dụ, khi khảo sát một nhóm người nhằm xác định tỷ lệ người ủng hộ một chính sách nhất định, phân phối nhị thức giúp phân tích xác suất thành công của từng câu trả lời. Việc này không chỉ giúp các nhà nghiên cứu hiểu rõ hơn về mẫu nghiên cứu mà còn hỗ trợ trong việc xây dựng các chiến lược truyền thông hiệu quả.
Trong lĩnh vực y tế, phân phối nhị thức được áp dụng khi thiết kế các thử nghiệm lâm sàng để xác định tính hiệu quả của một loại thuốc mới. Ví dụ, nếu một nghiên cứu quyết định về sự thành công hay không của một phương pháp điều trị, khả năng điều trị thành công có thể được mô hình hóa bằng phân phối nhị thức để tính toán rủi ro và lợi ích cho bệnh nhân.
Ngoài ra, trong lĩnh vực tài chính, phân phối nhị thức cũng được sử dụng để phân tích rủi ro. Các nhà đầu tư thường cần dự đoán khả năng thành công hoặc thất bại của các khoản đầu tư nhất định, và phân phối nhị thức hỗ trợ trong việc đánh giá các kịch bản khác nhau dựa vào các yếu tố như lợi nhuận hoặc thua lỗ. Thông qua việc hiểu và áp dụng phân phối nhị thức, các nhà hoạch định chính sách và nhà nghiên cứu có thể đưa ra quyết định đúng đắn hơn trong các lĩnh vực đa dạng này.