V.3c Ước lượng tham số hồi quy logistic

by Kurious Fox

Trong hồi quy logistic, ta cần tìm vector tham số $w$ (và bias $b$ ) sao cho mô hình dự đoán xác suất $p(x)$ khớp tốt nhất với dữ liệu quan sát.

🔎 1. Hàm xác suất (Likelihood)

Với dữ liệu $\{(x_i, y_i)\}_{i=1}^n$ , trong đó $y_i \in \{0,1\}$ :

$P(y_i \mid x_i; w) = p(x_i)^{y_i} \cdot (1 - p(x_i))^{1-y_i}$

Trong đó:

$p(x_i) = \sigma(w^T x_i + b) = \frac{1}{1 + e^{-(w^T x_i + b)}}$

Hàm likelihood cho toàn bộ dữ liệu:

$L(w) = \prod_{i=1}^n p(x_i)^{y_i} \cdot (1 - p(x_i))^{1-y_i}$

🔎 2. Hàm log-likelihood

Để dễ tính toán, lấy log:

$\ell(w) = \sum_{i=1}^n \Big[ y_i \log p(x_i) + (1-y_i)\log(1-p(x_i)) \Big]$

🔎 3. Hàm mất mát (Loss function)

Trong học máy, ta thường dùng negative log-likelihood (hay cross-entropy loss):

$J(w) = -\ell(w) = - \sum_{i=1}^n \Big[ y_i \log p(x_i) + (1-y_i)\log(1-p(x_i)) \Big]$

Mục tiêu: tối thiểu hóa $J(w)$ .

🔎 4. Ước lượng tham số

Không có công thức đóng (closed-form) như hồi quy tuyến tính.
Thường dùng phương pháp tối ưu số:
Gradient Descent: cập nhật tham số theo đạo hàm của hàm mất mát.
Stochastic Gradient Descent (SGD): cập nhật theo từng mẫu hoặc mini-batch.
Newton-Raphson / Iteratively Reweighted Least Squares (IRLS): dùng ma trận Hessian để hội tụ nhanh hơn.

Gradient của hàm mất mát:

$\nabla J(w) = \sum_{i=1}^n (p(x_i) - y_i) \cdot x_i$

Cập nhật tham số:

$w \leftarrow w - \eta \cdot \nabla J(w)$

Trong đó $\eta$ là learning rate.

🌍 Ý nghĩa

Hồi quy logistic thực chất là ước lượng tham số bằng Maximum Likelihood Estimation (MLE).
Các thuật toán tối ưu như Gradient Descent giúp tìm bộ tham số 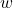$w$ tốt nhất để mô hình dự đoán xác suất chính xác.

Related

Leave a ReplyCancel reply

error: Content is protected !!