Không gian vectơ (vector space), còn gọi là không gian tuyến tính, là một khái niệm cơ bản trong toán học, đặc biệt là đại số tuyến tính. Nó là một tập hợp các đối tượng gọi là vectơ, cùng với hai phép toán: cộng vectơ và nhân vô hướng, thỏa mãn một số quy tắc nhất định.
Định nghĩa chính thức:
Một không gian vectơ ![]() trên một trường
trên một trường ![]() (ví dụ như tập số thực
(ví dụ như tập số thực ![]() hoặc số phức
hoặc số phức ![]() ) là một tập hợp được trang bị hai phép toán:
) là một tập hợp được trang bị hai phép toán:
- Cộng vectơ: Kết hợp hai vectơ
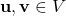 để tạo ra một vectơ mới
để tạo ra một vectơ mới  .
. - Nhân vô hướng: Nhân một số vô hướng
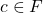 với một vectơ
với một vectơ  để tạo ra vectơ mới
để tạo ra vectơ mới  .
.
Cụ thể hơn là phải thỏa mãn các tiên đề (axiom) sau:
Các tiên đề của không gian vectơ:
- Tính đóng:
- Nếu
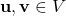 thì
thì  .
. - Nếu
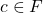 và
và  thì
thì  .
.
- Tính kết hợp của phép cộng:
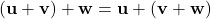 .
. - Tính giao hoán của phép cộng:
 .
. - Vectơ không:
Tồn tại một vectơ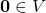 sao cho
sao cho  với mọi
với mọi  .
. - Vectơ đối:
Với mỗi , tồn tại
, tồn tại  sao cho
sao cho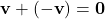 .
. - Tính phân phối:
 .
.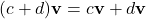 .
.
- Tính kết hợp của phép nhân vô hướng:
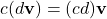 .
. - Phần tử đơn vị của phép nhân vô hướng:
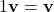 , với
, với 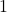 là phần tử đơn vị của trường
là phần tử đơn vị của trường 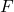 .
.
Ví dụ về không gian vectơ:
- Không gian tọa độ thực:
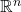 (tập các bộ
(tập các bộ 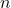 số thực) là một không gian vectơ trên
số thực) là một không gian vectơ trên 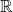 .
.
- Đa thức:
- Tập tất cả các đa thức có hệ số thực là một không gian vectơ.
- Ma trận:
- Tập các ma trận kích thước
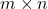 là một không gian vectơ.
là một không gian vectơ.
- Hàm số:
- Tập các hàm số giá trị thực là một không gian vectơ.
Kiểm tra: Không gian tọa độ thực 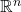 là một không gian vectơ
là một không gian vectơ
1. Mô tả 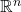
( \mathbb{R}^n\) là tập hợp tất cả các bộ ![]() số thực:
số thực:
![]()
Phép cộng vectơ:
![]()
Phép nhân vô hướng:
![]()
2. Kiểm tra các tiên đề của không gian vectơ
(1) Đóng với phép cộng
Tổng của hai vectơ trong ![]() vẫn là một vectơ trong
vẫn là một vectơ trong ![]() . ✔️
. ✔️
(2) Đóng với phép nhân vô hướng
Nhân một vectơ trong ![]() với một số thực vẫn cho ra vectơ trong
với một số thực vẫn cho ra vectơ trong ![]() . ✔️
. ✔️
(3) Tính kết hợp của phép cộng
![]()
Do phép cộng trong
(4) Tính giao hoán của phép cộng
![]()
Do phép cộng trong
(5) Phần tử không (vectơ không)
Vectơ
![]()
thỏa mãn
(6) Phần tử đối
Với mỗi vectơ ![]() , tồn tại
, tồn tại
![]()
sao cho
(7) Tính phân phối
![]()
![]()
Do tính chất phân phối trong
(8) Tính kết hợp của phép nhân vô hướng
![]()
✔️
(9) Phần tử đơn vị của phép nhân vô hướng
![]()
✔️
Kết luận
Vì ![]() thỏa mãn tất cả các tiên đề của không gian vectơ, nên:
thỏa mãn tất cả các tiên đề của không gian vectơ, nên:
*** QuickLaTeX cannot compile formula:
\[ \boxed{\mathbb{R}^n\]
*** Error message:
File ended while scanning use of \boxed.
Emergency stop.
là một không gian vectơ trên ![]()
theo