Hãy tưởng tượng đường thẳng như một “con đường” mà các điểm số của bạn đang đi dạo, còn độ dốc là mức độ “nghiêng” của con đường đó – giống như đang leo dốc hay trượt patin!
1. Độ dốc (hệ số góc) là gì?
Độ dốc (hay hệ số góc, ký hiệu thường là m) cho biết con đường số học của chúng ta nghiêng bao nhiêu. Nếu dốc càng “chóng mặt” thì đường càng đứng, còn nếu dốc thoải thì đường nằm gần ngang.
Công thức tính độ dốc:
Nếu có hai điểm trên đường thẳng là ![]() và
và ![]() , độ dốc được tính bằng:
, độ dốc được tính bằng:![]()
Ý nghĩa: ![]() là tỉ lệ thay đổi của
là tỉ lệ thay đổi của ![]() khi
khi ![]() thay đổi. Nói cách khác, nếu bạn đi 1 bước ngang (theo
thay đổi. Nói cách khác, nếu bạn đi 1 bước ngang (theo ![]() ), bạn sẽ “leo” hoặc “trượt” bao nhiêu theo chiều dọc (theo
), bạn sẽ “leo” hoặc “trượt” bao nhiêu theo chiều dọc (theo ![]() ).
).
- Nếu
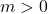 : Đường đang “leo núi” (nghiêng lên).
: Đường đang “leo núi” (nghiêng lên). - Nếu
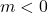 : Đường đang “trượt dốc” (nghiêng xuống).
: Đường đang “trượt dốc” (nghiêng xuống). - Nếu
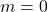 : Đường phẳng lì như xa lộ, không lên không xuống.
: Đường phẳng lì như xa lộ, không lên không xuống. - Nếu
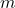 không xác định (vì mẫu số bằng 0): Đường thẳng đứng như cột điện!
không xác định (vì mẫu số bằng 0): Đường thẳng đứng như cột điện!
2. Phương trình đường thẳng
Phương trình đường thẳng là “bản đồ” giúp bạn vẽ con đường số học. Có nhiều dạng, nhưng dạng phổ biến và dễ nhớ nhất là:
Dạng tổng quát: ![]()
Dạng chính tắc (dạng y = mx + b):![]()
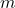 : Độ dốc (hệ số góc).
: Độ dốc (hệ số góc).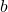 : Tung độ gốc, tức là điểm mà đường thẳng cắt trục
: Tung độ gốc, tức là điểm mà đường thẳng cắt trục 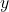 (khi
(khi 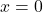 ). Nghĩ
). Nghĩ 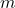 như “tính cách” của con đường (nghiêng nhiều hay ít), còn
như “tính cách” của con đường (nghiêng nhiều hay ít), còn 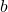 như “điểm xuất phát” trên trục
như “điểm xuất phát” trên trục 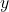 .
.
3. Ví dụ cụ thể
Hãy tưởng tượng bạn là một nhà thám hiểm đang vẽ bản đồ con đường từ điểm A(1, 2) đến điểm B(3, 6).
Bước 1: Tính độ dốc ![]()
Sử dụng công thức:![]()
- Độ dốc
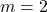 , nghĩa là cứ mỗi bước đi ngang 1 đơn vị, bạn “leo” lên 2 đơn vị. Con đường này khá dốc, như leo đồi!
, nghĩa là cứ mỗi bước đi ngang 1 đơn vị, bạn “leo” lên 2 đơn vị. Con đường này khá dốc, như leo đồi!
Bước 2: Tìm phương trình đường thẳng
Dùng dạng ![]() . Ta đã có
. Ta đã có ![]() . Giờ tìm
. Giờ tìm ![]() bằng cách thế một điểm, ví dụ
bằng cách thế một điểm, ví dụ ![]() , vào phương trình:
, vào phương trình:![]()
Vậy phương trình đường thẳng là:![]()
(Nếu ![]() , đường đi qua gốc tọa độ
, đường đi qua gốc tọa độ ![]() ).
).
Bước 3: Kiểm tra
Thử điểm ![]() :
:![]() : đúng
: đúng
Đường thẳng này đi qua cả hai điểm ![]() và
và ![]() .
.
Hãy hình dung con đường này như một chiếc cầu thang nghiêng, mỗi bước ngang 1 mét thì bạn phải “trèo” lên 2 mét. Nếu lười leo, bạn sẽ cần… thang máy!
4. Minh họa thêm
Nếu ![]() : Giả sử đường thẳng đi qua
: Giả sử đường thẳng đi qua ![]() và
và ![]() :
:![]()
Phương trình: ![]() . Vì đi qua
. Vì đi qua ![]() , ta có
, ta có ![]() . Đây là đường nằm ngang, như mặt hồ phẳng lặng.
. Đây là đường nằm ngang, như mặt hồ phẳng lặng.
Nếu ![]() không xác định: Giả sử đường qua
không xác định: Giả sử đường qua ![]() và
và ![]() :
:![]() : không xác định
: không xác định
Phương trình: ![]() . Đây là đường thẳng đứng, như cột cờ!
. Đây là đường thẳng đứng, như cột cờ!
Tóm lại
Độ dốc ![]() : Đo mức nghiêng của con đường số học.
: Đo mức nghiêng của con đường số học.
Phương trình ![]() : Bản đồ dẫn bạn qua các điểm trên đường.
: Bản đồ dẫn bạn qua các điểm trên đường.
Ví dụ: Từ ![]() đến
đến ![]() , ta có
, ta có ![]() , phương trình
, phương trình ![]() .
.