Số hữu tỷ là số có thể biểu diễn dưới dạng phân số 
, trong đó a (tử số) và b (mẫu số) là các số nguyên, và b phải khác 0.
Tập hợp các số hữu tỷ được ký hiệu là Q.
Nói một cách đơn giản, bất kỳ số nào có thể viết được dưới dạng thương của hai số nguyên đều là số hữu tỷ.
Các dạng của số hữu tỷ
Số hữu tỷ bao gồm nhiều loại số mà chúng ta thường gặp:
- Số nguyên: Mọi số nguyên đều là số hữu tỷ vì chúng có thể được viết dưới dạng phân số với mẫu số là 1.
- Ví dụ:
; 
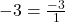
- Ví dụ:
- Phân số: Đây là dạng cơ bản nhất của số hữu tỷ.
- Ví dụ:
; 
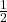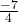
- Ví dụ:
- Số thập phân hữu hạn (có giới hạn): Những số này có thể dễ dàng chuyển thành phân số.
- Ví dụ:
; 
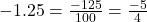
- Ví dụ:
- Số thập phân vô hạn tuần hoàn: Các số có một chữ số hoặc một cụm chữ số lặp đi lặp lại mãi mãi cũng là số hữu tỷ.
- Ví dụ:
; 
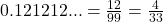
- Ví dụ:
Số nào không phải là số hữu tỷ? 🤔
Những số không thể biểu diễn được dưới dạng phân số được gọi là số vô tỷ. Các số này thường là các số thập phân vô hạn không tuần hoàn.
- Ví dụ về số vô tỷ:
- Số Pi (π) ≈ 3.14159…
- Căn bậc hai của 2 (
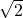) ≈ 1.41421…