Số thực – Số ảo – Cùng Học Cùng Mơ

Spread the love

Số thực là tất cả các số trên trục số, còn số ảo là số được tạo ra từ căn bậc hai của một số âm. Khi kết hợp cả hai, chúng ta có số phức.

Số Thực (R) 💡

Số thực là tất cả các số mà bạn có thể tìm thấy trên một trục số vô hạn. Về cơ bản, đó là mọi con số bạn thường nghĩ đến.

Tập hợp số thực, ký hiệu là R, bao gồm:

Số nguyên: …, -2, -1, 0, 1, 2, …
Phân số: $\frac{1}{2}, \frac{-3}{4}$
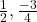
Số thập phân: 0.5, -1.25
Số vô tỷ (số thập phân vô hạn không tuần hoàn): 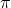$\pi$ (Pi), 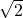$\sqrt{2}$

Hãy tưởng tượng một cây thước kẻ kéo dài vô tận, mọi điểm trên đó đều tương ứng với một số thực.

Số Ảo 🌀

Số ảo ra đời để giải quyết một vấn đề toán học không thể giải quyết trong tập hợp số thực: căn bậc hai của một số âm.

Đơn vị ảo cơ bản là i, được định nghĩa là:

$i = \sqrt{-1}$

Từ định nghĩa này, ta có một tính chất quan trọng: $i^2 = -1$ .

Một số ảo là một số thực b nhân với đơn vị ảo i, có dạng là bi.

Ví dụ: $2i$ , $-5i$ , $i\sqrt{3}$ .

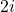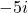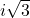Nếu số thực nằm trên một đường thẳng ngang, bạn có thể hình dung số ảo nằm trên một đường thẳng dọc vuông góc với nó.

Sự Kết Hợp: Số Phức (C) 🌐

Khi bạn kết hợp một số thực và một số ảo, bạn sẽ có một số phức. Tập hợp số phức được ký hiệu là C.

Nó có dạng chuẩn là:

$z = a + bi$

Trong đó:

a là phần thực.
b là phần ảo.

Ví dụ:

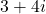$3 + 4i$ (phần thực là 3, phần ảo là 4)
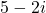$5 - 2i$ (phần thực là 5, phần ảo là -2)
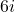$6i$ (phần thực là 0, phần ảo là 6) – Đây là một số thuần ảo.
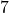$7$ (phần thực là 7, phần ảo là 0) – Mọi số thực cũng là số phức.

Nếu số thực nằm trên trục ngang (trục hoành) và số ảo nằm trên trục dọc (trục tung), thì mỗi số phức là một điểm trên một mặt phẳng hai chiều được gọi là mặt phẳng phức.

Trong khi ứng dụng của số thực có ở khắp mọi nơi (đo lường, tài chính, v.v.), các số ảo và số phức cũng có những ứng dụng cực kỳ quan trọng trong thế giới thực, đặc biệt là trong các lĩnh vực khoa học và kỹ thuật.

Chúng là một công cụ toán học mạnh mẽ để mô tả những thứ có cả độ lớn và pha (hoặc sự xoay), như sóng điện hoặc sóng âm.

Ứng dụng của Số Phức (bao gồm Số Ảo)

Kỹ thuật Điện và Điện tử 🔌

Đây là một trong những ứng dụng phổ biến nhất. Trong mạch điện xoay chiều (AC), dòng điện và điện áp liên tục thay đổi hướng. Số phức (dưới dạng “phasor”) giúp các kỹ sư dễ dàng tính toán các đại lượng có cả độ lớn và góc pha, như trở kháng. Việc này đơn giản hóa rất nhiều các phép tính phức tạp.

Xử lý Tín hiệu 🎵

Mọi tín hiệu kỹ thuật số—như sóng Wi-Fi, tín hiệu điện thoại, âm thanh trong file MP3, hay hình ảnh JPEG—đều có thể được phân tích bằng một công cụ gọi là Phép biến đổi Fourier. Phép biến đổi này sử dụng số phức để tách một tín hiệu phức tạp thành các sóng hình sin đơn giản. Điều này là nền tảng cho việc nén dữ liệu, lọc nhiễu và truyền thông không dây.

Cơ học Lượng tử ⚛️

Ở cấp độ cơ bản nhất của vũ trụ, các hạt như electron không tồn tại ở một vị trí cố định. Thay vào đó, chúng được mô tả bằng một “hàm sóng”, và phương trình cốt lõi của cơ học lượng tử (phương trình Schrödinger) bắt buộc phải sử dụng số phức. Phần thực và phần ảo của hàm sóng này liên quan đến xác suất tìm thấy hạt tại một vị trí nhất định.

Cơ học Lưu chất và Hàng không ✈️

Các nhà khoa học và kỹ sư sử dụng số phức để mô tả và phân tích dòng chảy của chất lỏng và không khí. Ví dụ, chúng có thể được dùng để mô hình hóa dòng không khí di chuyển qua cánh máy bay, giúp thiết kế hình dạng khí động học hiệu quả hơn.

Đồ họa Máy tính và Nghệ thuật 🖼️

Những hình ảnh fractal tuyệt đẹp và phức tạp vô hạn, như tập hợp Mandelbrot, được tạo ra bằng cách lặp đi lặp lại một phép tính đơn giản trên các số phức. Mỗi điểm trên mặt phẳng phức được kiểm tra xem nó có “hội tụ” hay “phân kỳ” khi lặp lại phép tính, tạo ra những hoa văn toán học độc đáo.

Tóm lại, dù không thể “cầm” hay “đo” được 3+4i mét, số phức là một công cụ không thể thiếu, giúp đơn giản hóa và giải quyết nhiều vấn đề thực tế liên quan đến sóng, dao động và các hệ thống thay đổi theo chu kỳ.

Discover more from Cùng Học Cùng Mơ

Subscribe to get the latest posts sent to your email.

Số thực – Số ảo