Thiết lập dạng ma trận cho hồi quy đa biến là cách biểu diễn mô hình hồi quy tuyến tính nhiều biến dưới dạng đại số tuyến tính, giúp việc tính toán và ước lượng trở nên gọn gàng và dễ xử lý hơn — đặc biệt khi dùng phương pháp bình phương nhỏ nhất (OLS).


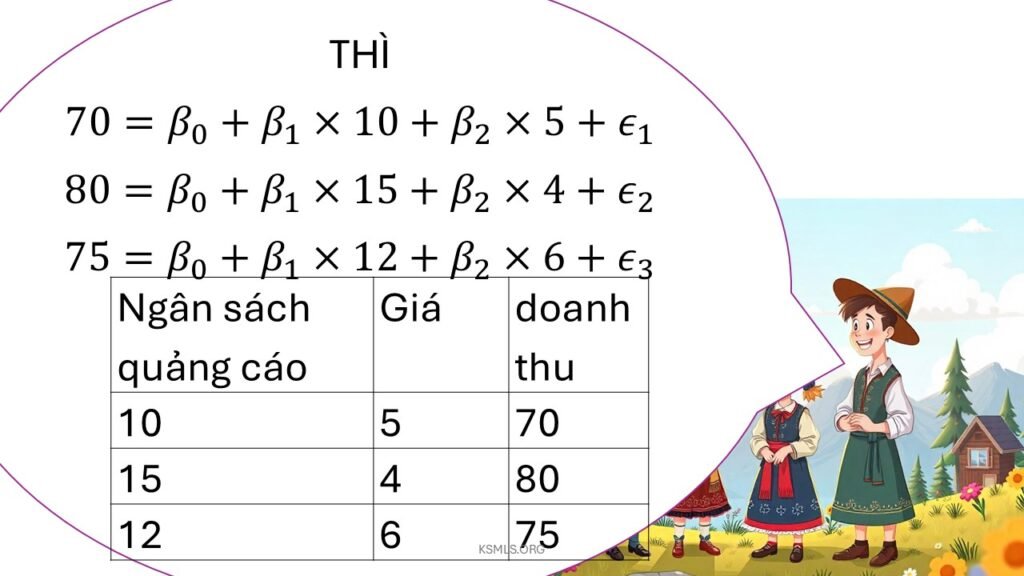





🧠 Mô hình hồi quy đa biến tổng quát
Giả sử ta có:
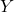 : biến phụ thuộc (vector cột kích thước
: biến phụ thuộc (vector cột kích thước 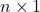 )
)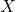 : ma trận các biến độc lập (kích thước
: ma trận các biến độc lập (kích thước 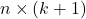 , với cột đầu tiên là toàn số 1 để ước lượng hệ số chặn)
, với cột đầu tiên là toàn số 1 để ước lượng hệ số chặn)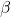 : vector hệ số hồi quy (kích thước
: vector hệ số hồi quy (kích thước 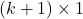 )
) : vector sai số (kích thước
: vector sai số (kích thước 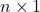 )
)
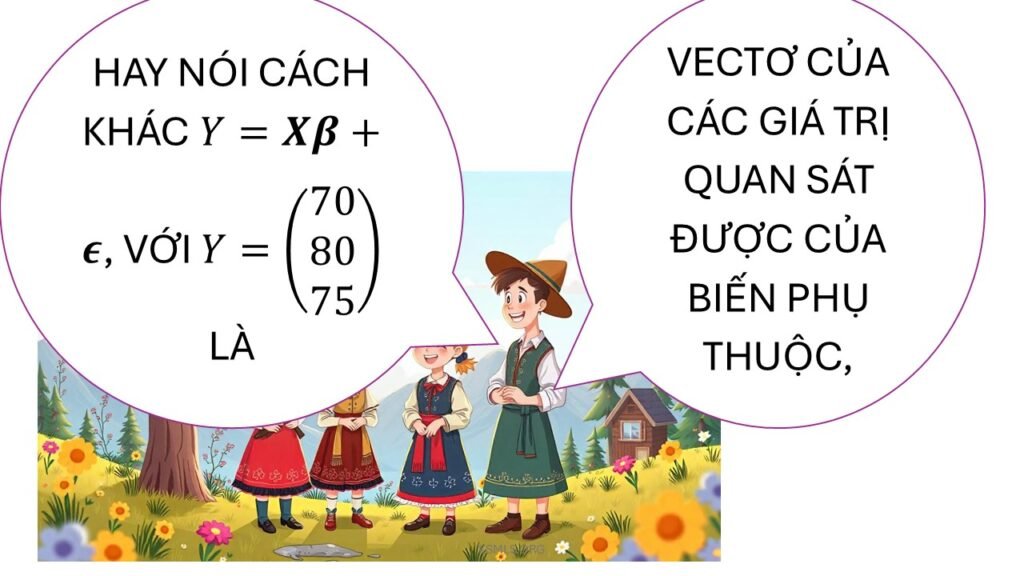
Ta biểu diễn mô hình như sau:
![]()
🔧 Cấu trúc ma trận
| Thành phần | Ký hiệu | Kích thước | Ý nghĩa |
|---|---|---|---|
| Biến phụ thuộc | Giá trị thực tế | ||
| Biến độc lập | Bao gồm cột 1s và các biến | ||
| Hệ số hồi quy | Các hệ số cần ước lượng | ||
| Sai số | Phần dư chưa giải thích |
🧮 Ước lượng bằng phương pháp OLS
Mục tiêu: tìm ![]() sao cho tổng bình phương sai số là nhỏ nhất:
sao cho tổng bình phương sai số là nhỏ nhất:
![]()
Sau khi có ![]() , ta có thể tính:
, ta có thể tính:
Dự đoán: ![]()
Phần dư: ![]()
