Để thiết lập phương trình đường thẳng dựa trên hệ số góc (độ dốc), ta cần hiểu rõ rằng phương trình đường thẳng thường được viết dưới dạng y = mx + b, trong đó:
m: Hệ số góc (độ dốc), cho biết mức độ nghiêng của đường thẳng.
b: Tung độ gốc, là giá trị của ![]() khi
khi ![]() .
.
Để thiết lập phương trình, ta cần ít nhất hệ số góc ![]() và một điểm mà đường thẳng đi qua hoặc tung độ gốc
và một điểm mà đường thẳng đi qua hoặc tung độ gốc ![]() .
.
1. Trường hợp: Biết hệ số góc ![]() và một điểm trên đường thẳng
và một điểm trên đường thẳng
Giả sử bạn biết hệ số góc ![]() và một điểm
và một điểm ![]() mà đường thẳng đi qua. Phương trình đường thẳng được thiết lập bằng cách:
mà đường thẳng đi qua. Phương trình đường thẳng được thiết lập bằng cách:
- Dùng dạng
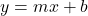 .
. - Thay
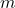 và điểm
và điểm 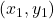 vào để tìm
vào để tìm 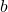 .
. - Viết lại phương trình hoàn chỉnh.
Ví dụ 1:
Cho hệ số góc ![]() và đường thẳng đi qua điểm
và đường thẳng đi qua điểm ![]() .
.
- Bước 1: Dùng dạng
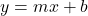 , thay
, thay 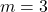 :
: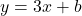
- Bước 2: Thay điểm
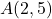 vào để tìm
vào để tìm 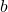 :
: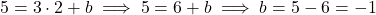
- Bước 3: Phương trình đường thẳng là:
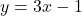
Đường này như một con dốc nghiêng (m = 3, khá dốc!), bắt đầu từ điểm thấp hơn trục ![]() một chút (b = -1). Tưởng tượng bạn đang trượt ván trên con dốc này, mỗi bước ngang 1 mét thì bạn “lao” lên 3 mét!
một chút (b = -1). Tưởng tượng bạn đang trượt ván trên con dốc này, mỗi bước ngang 1 mét thì bạn “lao” lên 3 mét!
2. Trường hợp: Biết hệ số góc ![]() và tung độ gốc
và tung độ gốc ![]()
Nếu biết cả ![]() và
và ![]() , bạn chỉ cần thay trực tiếp vào phương trình
, bạn chỉ cần thay trực tiếp vào phương trình ![]() .
.
Ví dụ 2:
Cho ![]() và đường thẳng cắt trục
và đường thẳng cắt trục ![]() tại
tại ![]() .
.
- Phương trình đường thẳng là:
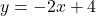
Đây là một con dốc “trượt xuống” (vì ![]() ), bắt đầu từ điểm
), bắt đầu từ điểm ![]() trên trục
trên trục ![]() . Tưởng tượng bạn đang trượt tuyết, mỗi bước ngang 1 mét thì bạn tụt xuống 2 mét! Nhưng hy vọng đây không phải điểm môn toán của bạn!
. Tưởng tượng bạn đang trượt tuyết, mỗi bước ngang 1 mét thì bạn tụt xuống 2 mét! Nhưng hy vọng đây không phải điểm môn toán của bạn!
3. Trường hợp: Biết hệ số góc ![]() và đường thẳng đi qua gốc tọa độ
và đường thẳng đi qua gốc tọa độ
Nếu đường thẳng đi qua gốc tọa độ ![]() , thì
, thì ![]() , và phương trình đơn giản là:
, và phương trình đơn giản là:![]()
Ví dụ 3:
Cho ![]() và đường thẳng đi qua gốc
và đường thẳng đi qua gốc ![]() .
.
- Phương trình đường thẳng:
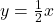
Con đường này như một con dốc nhẹ nhàng, đi qua “trạm gốc” ![]() . Cứ đi ngang 2 mét thì bạn chỉ “leo” lên 1 mét – một chuyến đi bộ thư giãn!
. Cứ đi ngang 2 mét thì bạn chỉ “leo” lên 1 mét – một chuyến đi bộ thư giãn!
4. Trường hợp đặc biệt: Đường thẳng đứng
Nếu hệ số góc ![]() không xác định (vì đường thẳng song song với trục
không xác định (vì đường thẳng song song với trục ![]() ), phương trình không có dạng
), phương trình không có dạng ![]() . Thay vào đó, nó có dạng:
. Thay vào đó, nó có dạng:![]()
trong đó ![]() là hoành độ của điểm mà đường thẳng đi qua.
là hoành độ của điểm mà đường thẳng đi qua.
Ví dụ 4:
Cho đường thẳng có hệ số góc không xác định và đi qua điểm ![]() .
.
- Vì hệ số góc không xác định, đường thẳng song song với trục
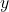 , nên phương trình là:
, nên phương trình là: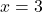
Đường này như một cột điện thẳng đứng, không nghiêng ngả, chỉ đứng yên tại ![]() . Bạn không thể leo dốc, chỉ có thể… đứng ngắm!
. Bạn không thể leo dốc, chỉ có thể… đứng ngắm!
Tóm lại quy trình thiết lập phương trình đường thẳng dựa trên hệ số góc:
- Xác định
 : Hệ số góc cho biết độ nghiêng.
: Hệ số góc cho biết độ nghiêng. - Tìm
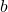 : Dùng một điểm trên đường thẳng hoặc tung độ gốc.
: Dùng một điểm trên đường thẳng hoặc tung độ gốc. - Viết phương trình: Thay
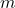 và
và 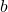 vào
vào 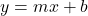 , hoặc dùng dạng phù hợp (như
, hoặc dùng dạng phù hợp (như 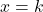 nếu thẳng đứng).
nếu thẳng đứng). - Kiểm tra: Thay điểm đã cho vào phương trình để đảm bảo đúng.
Ví dụ kiểm tra (dùng ví dụ 1):
Phương trình ![]() , kiểm tra với điểm
, kiểm tra với điểm ![]() :
:![]() (đúng)
(đúng)