







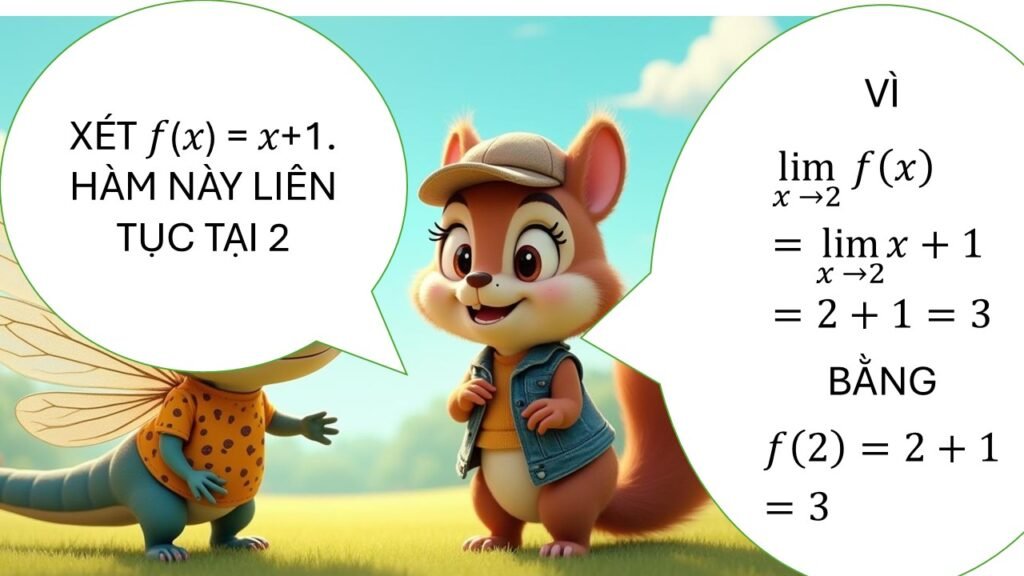


📌 Định nghĩa hàm liên tục tại một điểm
Hàm số ![]() được gọi là liên tục tại điểm
được gọi là liên tục tại điểm ![]() nếu thỏa mãn 3 điều kiện:
nếu thỏa mãn 3 điều kiện:
 xác định (tồn tại giá trị tại
xác định (tồn tại giá trị tại  ).
).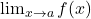 tồn tại.
tồn tại.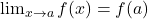 .
.
👉 Nói cách khác: giá trị của hàm tại điểm đó bằng với giới hạn khi tiến tới điểm đó.
📌 Ý nghĩa trực quan
- Đồ thị của hàm số liên tục không bị đứt đoạn, không nhảy cóc, không có lỗ hổng.
- Khi vẽ, ta có thể “vẽ một nét bút liền” mà không cần nhấc bút.
📊 Ví dụ minh họa
Ví dụ 1: Hàm liên tục
![]()
- Với mọi
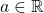 :
: .
.
👉 Hàm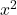 liên tục trên toàn bộ
liên tục trên toàn bộ 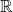 .
.
Ví dụ 2: Hàm không liên tục
![]()
- Tại
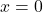 , hàm không xác định.
, hàm không xác định.
👉 Hàm này không liên tục tại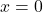 , nhưng liên tục trên
, nhưng liên tục trên  .
.
📌 Các loại gián đoạn thường gặp
Gián đoạn kiểu 1 (nhảy cóc): giới hạn trái và phải tồn tại nhưng khác nhau.
Gián đoạn kiểu 2: giới hạn không tồn tại.
Gián đoạn kiểu 3: hàm không xác định tại điểm đó.
📊 Ví dụ: Hàm liên tục
![]()
- Miền xác định:
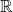 .
. - Miền giá trị:
 .
. - Đồ thị: đường cong parabol đi qua gốc tọa độ, trơn tru, không bị đứt đoạn.
👉 Khi vẽ, bạn có thể kéo một nét bút liền từ trái sang phải.
📊 Ví dụ: Hàm gián đoạn
![]()
- Miền xác định:
 .
. - Miền giá trị:
 .
. - Đồ thị: hai nhánh hyperbol, một ở góc phần tư I và một ở góc phần tư III.
👉 Tại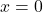 , hàm không xác định → đồ thị bị “đứt” bởi một đường tiệm cận đứng.
, hàm không xác định → đồ thị bị “đứt” bởi một đường tiệm cận đứng.
✨ Ý nghĩa trực quan
- Hàm liên tục: đồ thị không nhảy cóc, không lỗ hổng.
- Hàm gián đoạn: đồ thị bị đứt đoạn hoặc nhảy vọt tại một số điểm.
