11. hàm không liên tục

📌 Định nghĩa

Một hàm số không liên tục tại điểm nếu ít nhất một trong ba điều kiện liên tục không thỏa mãn:

1. không xác định.
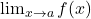2. không tồn tại.
3. .

👉 Nói cách khác: đồ thị hàm số bị đứt đoạn, nhảy cóc hoặc có lỗ hổng tại điểm đó.

📊 Các dạng gián đoạn thường gặp

Gián đoạn loại 1 (nhảy cóc):
Giới hạn trái và phải tồn tại nhưng khác nhau.
Ví dụ:

   

👉 Tại , hàm nhảy từ 1 lên 2.

Gián đoạn loại 2:
Giới hạn trái hoặc phải không tồn tại.
Ví dụ:

   

👉 Khi , hàm dao động vô hạn → không có giới hạn.

Gián đoạn loại 3 (hàm không xác định):
Hàm không có giá trị tại điểm đó.
Ví dụ:

   

👉 Tại , hàm không xác định → gián đoạn.

✨ Ý nghĩa trực quan

• Hàm liên tục: vẽ đồ thị bằng một nét bút liền.
• Hàm không liên tục: phải “nhấc bút” tại điểm gián đoạn.

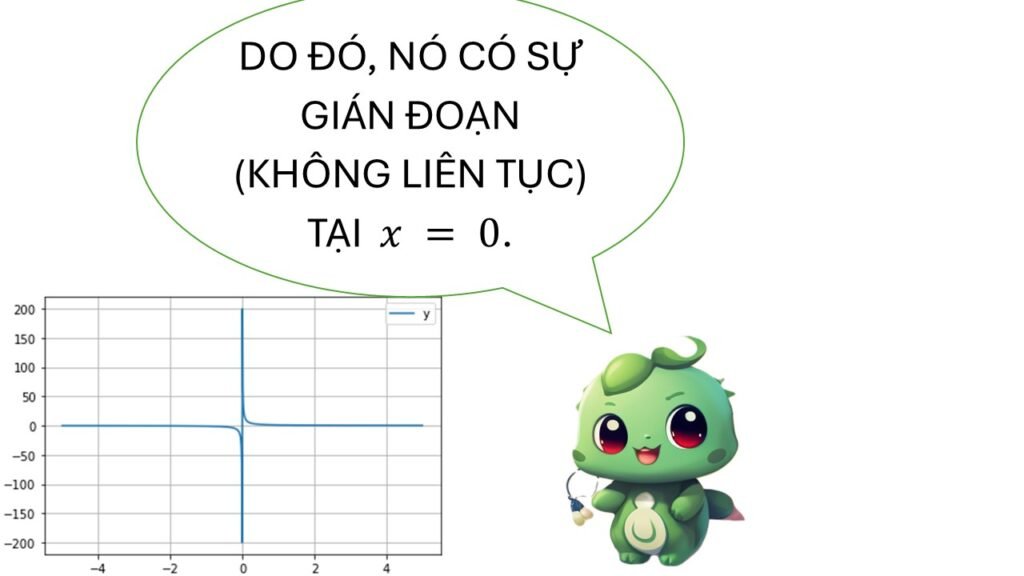
📊 Ví dụ: Hàm gián đoạn tại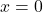

   

Miền xác định: .
Đặc điểm:

• Khi , .
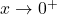• Khi , .
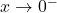  👉 Giới hạn trái và phải khác nhau → hàm không liên tục tại .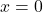

📌 Ý nghĩa trực quan

• Đồ thị gồm hai nhánh hyperbol:
• Một nhánh ở góc phần tư I (dương/dương).
• Một nhánh ở góc phần tư III (âm/âm).
• Tại 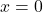, đồ thị bị “đứt” bởi một tiệm cận đứng.

✨ Tóm lại

• Hàm liên tục: vẽ đồ thị bằng một nét liền.
• Hàm không liên tục: phải “nhấc bút” tại điểm gián đoạn.

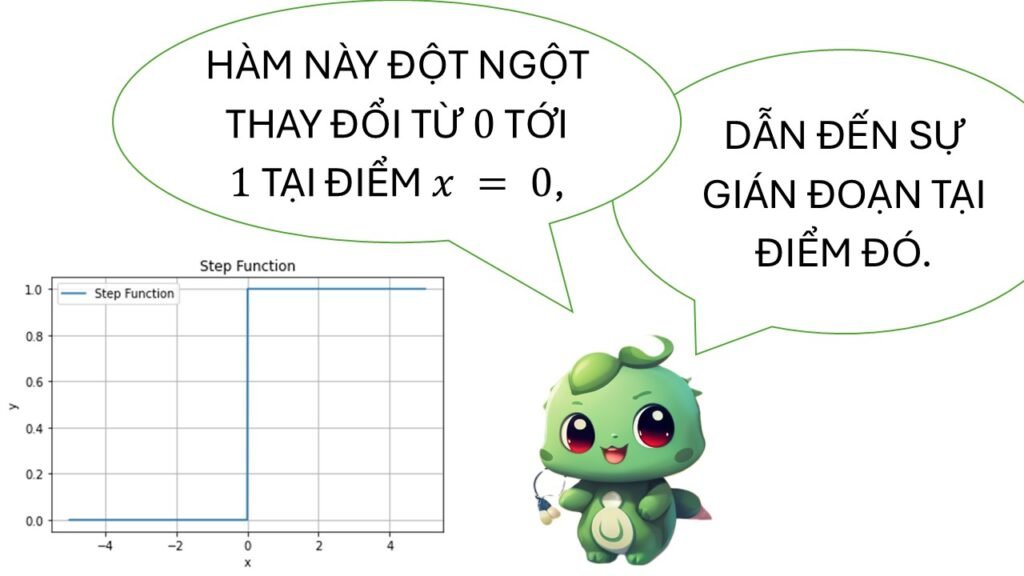
📊 Ví dụ: Hàm bậc thang (step function)

   

• Với , giá trị hàm luôn bằng 1 (một đường ngang).
• Với 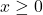, giá trị hàm luôn bằng 2 (một đường ngang khác).
• Tại 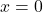, hàm “nhảy cóc” từ 1 lên 2.

👉 Đây chính là gián đoạn loại 1: giới hạn trái và phải tồn tại nhưng khác nhau.

✨ Ý nghĩa trực quan

• Đồ thị gồm hai đoạn thẳng song song với trục hoành, một nằm ở mức 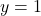, một ở mức .
• Tại điểm 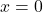, đồ thị bị “nhảy” lên → không thể vẽ bằng một nét liền.