




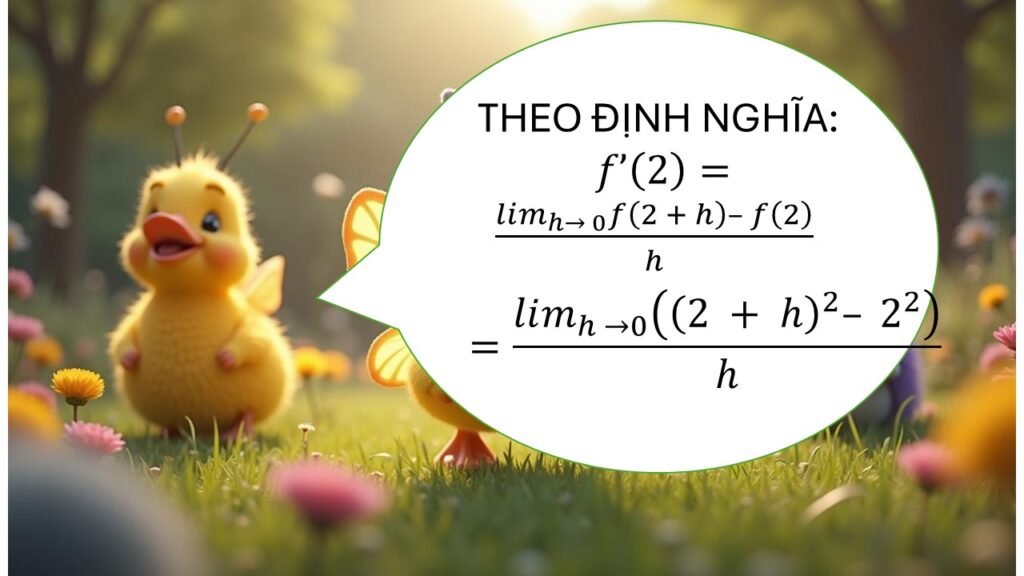


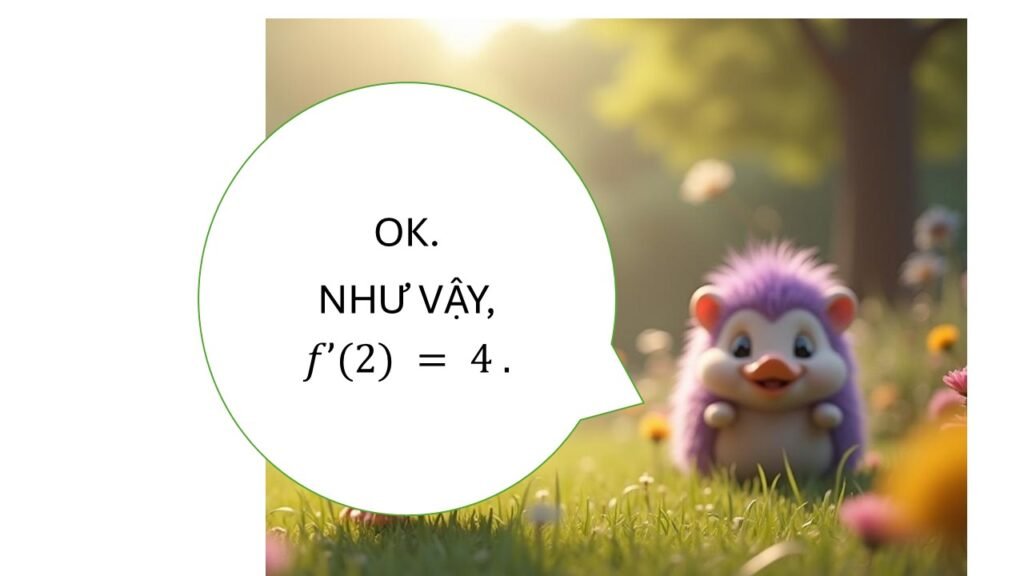





📌 Định nghĩa đạo hàm
Cho hàm số ![]() . Đạo hàm của
. Đạo hàm của ![]() tại điểm
tại điểm ![]() được định nghĩa là:
được định nghĩa là:
![]()
👉 Ý nghĩa: đạo hàm đo tốc độ thay đổi tức thời của hàm số tại điểm đó, hay chính là hệ số góc của tiếp tuyến với đồ thị hàm tại điểm ![]() .
.
📊 Ví dụ minh họa
Ví dụ 1: Hàm bậc hai
![]()
- Đạo hàm:
![Rendered by QuickLaTeX.com \[ f'(x) = 2x\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-a0f8b4eeff6d8cb4043fce9039a5e0c7_l3.png)
- Tại
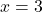 :
:![Rendered by QuickLaTeX.com \[ f'(3) = 6\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-c4c2963a50d4966cb6a5e18d37baea26_l3.png)
👉 Nghĩa là tại điểm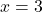 , đồ thị có tiếp tuyến với hệ số góc bằng 6.
, đồ thị có tiếp tuyến với hệ số góc bằng 6.
Ví dụ 2: Hàm lượng giác
![]()
- Đạo hàm:
![Rendered by QuickLaTeX.com \[ f'(x) = \cos x\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-2e01a5d83a8ce070dc080058df5ee36b_l3.png)
- Tại
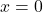 :
:![Rendered by QuickLaTeX.com \[ f'(0) = 1\]](https://vi.ksml4.com/wp-content/ql-cache/quicklatex.com-0f7a067336f1c52eab2475ff701384c3_l3.png)
👉 Tại gốc tọa độ, tiếp tuyến của đồ thị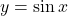 có hệ số góc bằng 1.
có hệ số góc bằng 1.
✨ Ý nghĩa thực tế
- Trong vật lý: đạo hàm biểu diễn vận tốc (tốc độ thay đổi của quãng đường theo thời gian).
- Trong kinh tế: đạo hàm biểu diễn tốc độ tăng trưởng.
- Trong hình học: đạo hàm cho ta tiếp tuyến của đồ thị.
