




📊 Ví dụ:
Cho hàm số
![]()
🔹 Bước 1: Tính đạo hàm
![]()
🔹 Bước 2: Giải phương trình 
![]()
👉 Đây là điểm nghi ngờ cực trị.
🔹 Bước 3: Dùng đạo hàm cấp hai
![]()
- Vì
 ⇒ tại
⇒ tại 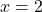 , hàm đạt cực đại.
, hàm đạt cực đại.
🔹 Bước 4: Tính giá trị cực đại
![]()
✅ Kết luận
- Hàm số có cực đại tại
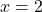 .
. - Giá trị cực đại là
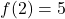 .
. - Đồ thị là một parabol úp xuống, đỉnh chính là điểm cực đại.
📊 Ví dụ 2:
Cho hàm số
![]()
🔹 Bước 1: Tính đạo hàm
![]()
🔹 Bước 2: Giải phương trình 
![]()
![]()
🔹 Bước 3: Dùng đạo hàm cấp hai
![]()
 ⇒
⇒ 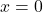 là cực tiểu
là cực tiểu ⇒
⇒ 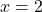 là cực đại
là cực đại
🔹 Bước 4: Tính giá trị cực trị
 ⇒ cực tiểu tại
⇒ cực tiểu tại 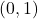
 ⇒ cực đại tại
⇒ cực đại tại 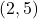
✅ Kết luận
- Hàm có cực tiểu tại (0,1)
- Hàm có cực đại tại (2,5)
